Der Quantenparallelismus öffnet den Quantencomputern Türen zu völlig neuen Rechenwegen. Die Vermutung liegt nahe, dass sie dadurch Grenzen der Berechenbarkeit für herkömmliche Computer spielend überflügeln können. Im Folgenden stelle ich Ihnen den berühmten Grover-Algorithmus für Quantencomputer im Detail vor. Er ist in der Lage sämtliche „Nadel im Heuhaufen“-Probleme drastisch schneller zu lösen, als ein herkömmlicher Computer. Dabei gehe ich auch kurz auf die Komplexitätstheorie ein, einem faszinierenden Teilgebiet der Informatik, und zeige Ihnen inwiefern selbst der Grover-Algorithmus an seine Komplexitätsgrenzen stößt.
Inhalt
- 1 Der Quantenparallelismus
- 2 Die NP-Probleme der Informatik
- 3 Der Quantencomputer: Die ultimative Brute Force – Lösung ?
- 4 Der Grover-Algorithmus
- 5 Ein Qubit und einfache Quantengatter
- 6 Geometrische Anschauung für den Grover-Algorithmus
- 7 Das Orakel: Eine einfache Spiegelung
- 8 Zwischenfazit: Die Stärken und Schwächen des Grover-Algorithmus
- 9 Der Grover-Algorithmus als Quanten-Schaltkreis
- 10 Ein Beispiel-Orakel für ein echtes „3SAT“-Problem
- 11 Fußnoten
Der Quantenparallelismus
Quantencomputer ermöglichen eine völlig neue Form des parallelen Rechnens: Dem Quantenparallelismus. Dadurch ist ein Quantencomputer in der Lage dasselbe Quantenprogramm für eine Vielzahl von Werten gleichzeitig durchzuführen, prinzipiell sogar für alle Werte die der Computer überhaupt darstellen kann. Dem Quantenparallelismus liegt ein Grundprinzip der Quantenmechanik zu Grunde: Dem sogenannten „Superpositionsprinzip“. D.h. jeder Quantencomputer besitzt den Quantenparallelismus automatisch von Grund auf.
Auf den ersten Blick besitzt der Quantenparallelismus ein unglaubliches Potential. Und seit den allerersten Anfängen der Quantencomputer fragen sich Wissenschaftler, ob sie damit sogar in der Lage sind den heiligen Gral der Computerwissenschaften zu finden: Einen einfachen Weg, um alle überhaupt möglichen „NP-Probleme“ zu lösen.
Die NP-Probleme der Informatik
In den 1960er Jahren fingen Computerwissenschaftler an Probleme in verschiedene Klassen zu unterteilen, je nachdem wie aufwendig sie zu lösen sind. Die Komplexitätsklasse $ P $ enthält grob gesprochen alle Probleme, die sich mithilfe eines herkömmlichen Computers relativ einfach lösen lassen. Genauer gesagt: mit „polynomialem Rechenaufwand“ i. Demgegenüber steht z.B. die Komplexitätsklasse $ NP $. Diese enthält alle Probleme, die sich zwar nicht einfach lösen lassen, deren Lösung man aber mithilfe eines herkömmlichen Computers einfach überprüfen kann, und zwar wieder mit polynomialem Aufwand. Jetzt sind gerade viele bedeutende Probleme der Informatik und Mathematik NP-Probleme. Ein Beispiel für ein NP-Problem ist etwa die bereits erwähnte Zerlegung in Primfaktoren: Wenn man einmal die gesuchten Primfaktoren $ p $ und $ q $ einer Zahl $ n $ gefunden hat, ist die Überprüfung der Lösung kinderleicht, nämlich gerade $ p*q = n $.
Wenn man es genau nimmt, hat die Unterteilung von Problemen in verschiedene Klassen fast schon philosophische Bedeutung: Durch sie konnte die Wissenschaft erstmals auf formale Weise ermitteln, welche Probleme einfach und welche besonders schwierig sind. Die verschiedenen Klassen geben dabei abgestufte Schwierigkeitsgrade an und zeigen Zusammenhänge auf.
Die Komplexitätstheorie ist ein sehr breites Teilgebiet der Informatik. Und in ihrem Zentrum steht eine alles überstrahlende Frage: Ist $ P = NP $ ? D.h. lassen sich diese schwierigen Probleme am Ende nicht doch einfach lösen? ii
Diese Frage ist so etwas wie der „Heilige Gral“ der Computerwissenschaften. Sie wurde u.a. im Jahr 2000 in die exklusive Liste der sieben Millennium-Probleme von offenen Rätseln in der Mathematik aufgenommen, deren Klärung eine enorme Tragweite hätte (nebenbei ist jedes Millenium-Problem mit einem Preisgeld von einer Millionen Euro dotiert). Falls $ P = NP $ wahr wäre, könnten wir beispielsweise mathematische Intuition mit einem Computer automatisieren iii. Diverse andere offene Probleme der Mathematik könnten so z.B. ebenfalls gelöst werden. Für die Wissenschaft als Ganzes hätte dies vermutlich monumentale Auswirkungen.
Allerdings gehen die meisten Experten davon aus, dass $ P = NP $ leider nicht wahr ist und dass sich die NP-Probleme nicht einfach mit einem herkömmlichen Computer lösen lassen.
Aber jetzt kommen die Quantencomputer ins Spiel. Für diese haben die Komplexitätstheoretiker eine neue Klasse von Problemen eingeführt: $ BQP $. Dies sind grob gesprochen wieder alle Probleme, die sich einfach mit einem Quantencomputer lösen lassen. Die Frage ist jetzt: Wenn schon nicht $ P = NP $ ist, ist dann wenigstens $ NP $ in $ BQP $ enthalten? Sind die NP-Probleme also leicht mit einem Quantencomputer zu lösen?
Der Quantencomputer: Die ultimative Brute Force – Lösung ?
Wie verhält es sich also mit den Quantencomputern und den NP-Problemen? Auf den ersten Blick scheint der Quantenparallelismus hierfür zu schön um wahr zu sein. Warum?
Die NP-Probleme sind ja gerade die Probleme, deren Lösung man einfach überprüfen kann. Und mit einem Quantencomputer können wir uns alle möglichen Lösungskandidaten prinzipiell gleichzeitig vornehmen und testen, ob sie das Problem lösen. Violà, wir haben einen ultimativen NP-Cruncher bzw. den ultimativen „Brute Force“ – Algorithmus gefunden, also einen Algorithmus der „brachial“ einfach alle möglichen Kombinationen ausprobiert.
Leider ist das nur auf den ersten Blick so einfach.
Tatsächlich vermuten die Komplexitätstheoretiker eher folgende Zusammenhänge zwischen den Klassen $ P $, $ NP $ und $ BQP $.
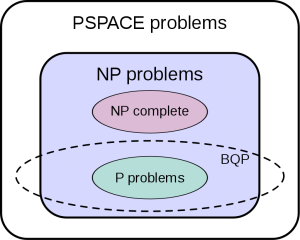
(Quelle: https://en.wikipedia.org/wiki/File:BQP_complexity_class_diagram.svg)
Das Diagramm zeigt den Zusammenhang der Komplexitätklassen, den die meisten Wissenschaftler vermuten iv. Der vollständigkeithalber sei erwähnt: „PSPACE“ sind die Probleme, für die der Speicherbedarf des Lösungsprogramms polynomial ansteigt, deren Laufzeit aber beliebig lang sein darf und evtl. nie endet. „NP complete“ sind die NP-Probleme, die repräsentativ für alle anderen NP-Probleme sind: Wenn man davon nur eines einfach lösen könnte, kann man alle anderen NP-Probleme auch einfach lösen, und entsprechend hätte man P = NP bewiesen.
Die Suche nach einem NP-Cruncher demonstriert sehr schön wie vielschichtig das Thema Quantencomputer ist und dass selbst die erstaunlichen Quantencomputer ihre Grenzen haben. Ich habe es deshalb ausgewählt, weil man an ihm die vielen Facetten der Quanten-Algorithmen ideal für Einsteiger verdeutlichen kann.
Der Grover-Algorithmus
Der Grover-Algorithmus wurde 1996 von dem indischen Informatiker Lov Grover gefunden. Er ist einer der Standard-Beispiele, die man als erstes lernt, wenn man sich näher mit Quanten-Algorithmen beschäftigt. Unter anderen auch, weil er so vielfältig einsetzbar ist. Normalerweise bekommt man erklärt, dass der Grover-Algorithmus für das komplette Durchsuchen einer Datenbank mittels eines sogenannten „Orakels“ verwendet wird, anders ausgedrückt: Um die Nadel im Heuhaufen zu finden. Dahinter verbirgt sich aber gerade auch die NP-Problematik: Zum einen haben wir eine riesige Menge an Lösungskandidaten, die unsere „Datenbank“ ist. Zum anderen haben wir eine einfache Prüfroutine, nämlich das „Orakel“, mit der wir feststellen können, ob ein Lösungskandidat tatsächlich eine Lösung ist v.
Wir wissen, dass ein Quantencomputer in der Lage ist alle Lösungskandidaten gleichzeitig durch die Prüfroutine durchzujagen. Die echten Lösungen werden dabei von der Routine erkannt. Die vertrackte Frage ist nun: Was bringt uns das eigentlich? Am Ende müssen wir ein Ergebnis messen, und wir erinnern uns, dass das bei Quantencomputern immer eine Sache der Wahrscheinlichkeit ist. Und dabei stören jetzt die falschen Lösungskandidaten wieder und verringern die Wahrscheinlichkeit die echte Lösung zu messen. Wir müssen es also irgendwie hinbekommen, dass der Quanten-Algorithmus die falschen Lösungskandidaten in den Qubit-Speicherregistern weitestgehend unterdrückt und am Ende die echte Lösung mit einer hohen Wahrscheinlichkeit gemessen wird. In dem wir die Prozedur dann mehrmals wiederholen wird aus der Wahrscheinlichkeit dann immer mehr Gewissheit.
Und das ist gerade die Herausforderung an den Quanten-Algorithmen: Die gewünschte Lösung muss zu einer globalen Eigenschaft der Qubit-Register werden. Als Hilfsmittel hat man dafür die Quantengatter, deren Arbeitsweise zwar genau bekannt ist, die aber leider alles andere als intuitiv und einfach sind.
Ein Qubit und einfache Quantengatter
Um die Quantencomputer im Allgemeinen und den Grover-Algorithmus im Besonderen einem breiteren Publikum näher zu bringen, verwende ich auf „quantencomputer-info.de“ eine vereinfachte Sichtweise auf die Qubits und die Quantengatter. In meinem Artikel Das Qubit und ein Magier bei „Britain Has Got Talent“ hatte ich schon die Zeigerbilder eingeführt mit denen wir uns die verschiedenen Zustände eines Qubits vorstellen können. Das Qubit ist dann ein Zeiger auf der Kreislinie in diesem Bild.
(„Disclaimer“: Falls Sie diesen Artikel zur Vorbereitung für eine Prüfung verwenden sollten, beachten Sie bitte, dass die Lehrbuch-Darstellung eines Qubits die „Blochkugel“ ist vi. Um den Grover-Algorithmus richtig zu verstehen, reicht meine einfache Sichtweise aber erstaunlicherweise aus).
Folgendes Zeigerbild zeigt ein Qubit, dass gleichzeitig im Zustand |0⟩ und im Zustand |1⟩ ist.
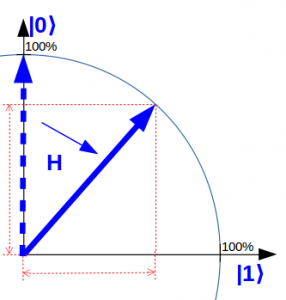
Das Besondere an diesem Bild ist außerdem, dass die Zustände |0⟩ und |1⟩ gleichmäßig überlagert sind. Es ist zu gleichen Teilen sowohl |0⟩ als auch |1⟩. Ein Qubit im Zustand |0⟩ gelangt in diesen Zustand der gleichmäßigen Überlagerung, indem es in dem einfachen Zeigerbild um 45° gedreht wird. Diese Drehung wird durch das Hadamard-Quantengatter H durchgeführt.
|qubit⟩ = H |0⟩
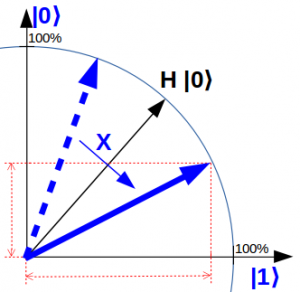
Ein anderes Gatter ist das X – Quantengatter. Es spiegelt das aktuelle Qubit an der Winkelhalbierenden, also gerade am Zustand H |0⟩. Oder anders betrachtet: Das X-Gatter tauscht den Zustand |0⟩ und den Zustand |1⟩ gegeneinander aus.
X |0⟩ = |1⟩ und X |1⟩ = |0⟩
Geometrische Anschauung für den Grover-Algorithmus
Das Schöne am Grover-Algorithmus ist auch, dass man ihn an einem einfachen geometrischen Zeigerbild erklären kann.
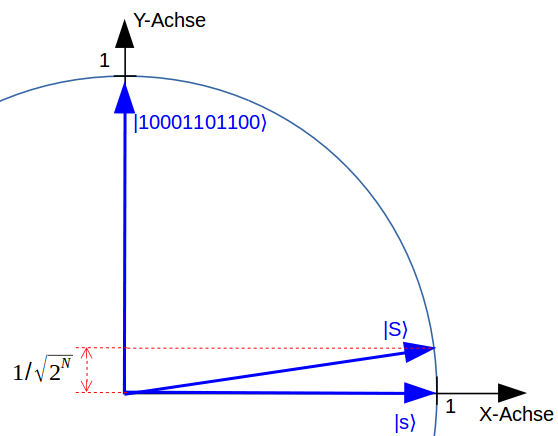
Wenn wir uns dafür ein ganzes Register mit N Qubits anschauen, so verhalten sich die Zustände in diesem Register auch wieder wie ein einziger Zeiger. Der Zeiger dreht sich allerdings nicht mehr in einer 2 dimensionalen Ebene, sondern in einem $ 2^N $ dimensionalem Raum! Jede Achse in diesem Raum entspricht einer anderen Kombination von 0en und 1en in dem Qubitregister: Eine Achse entspricht zum Beispiel der Kombination 10001101100, eine andere Achse entspricht der Kombination 00001101100, wieder eine andere Achse entspricht einer ganz anderen Kombination 11011010111 und so weiter. Zum Glück können wir diesen $ 2^N $ dimensionalen Raum für den Grover-Algorithmus wieder auf eine 2 dimensionale Ebene vereinfachen.
Dazu konstruieren wir drei Zeiger, die auf einer Kreislinie in einer Ebene liegen. Der erste Zeiger ist einfach: Nehmen wir mal an die erste Kombination 10001101100 löst das NP-Problem. Das wissen wir am Anfang natürlich noch nicht, wir könnten die Kombination auch „Lösung“ nennen. Die zugehörige Achse wird jetzt unsere Y-Achse.
Der zweite Zeiger zeigt in die Richtung der „gleichmäßigen Überlagerung“. Das ist gerade der Zeiger, der entsteht, wenn auf alle Qubits jeweils ein Hadamard-Quantengatter angewendet wird. Für ein Qubit hatten wir gerade gesehen, dass ein Hadamard-Quantengatter den Qubit-Zeiger so dreht, dass beide Zustände $ \rvert 0 \rangle $ und $ \rvert 1 \rangle $ gleichmäßig überlagert werden und gleichzeitig vorhanden sind. Wenn wir jeweils ein Hadamard-Gatter auf jedes Qubit anwenden bedeutet das, dass alle möglichen Zustände des ganzen Quantencomputers gleichmäßig überlagert sind. Das ist also genau die Situation, die wir für unseren Brute-Force-Plan benötigen: Wir haben alle möglichen Kombinationen von 0en und 1en, und somit die gesamte Menge an Lösungskandidaten, gleichzeitig im Zugriff.Nennen wir diesen Zeiger der gleichmäßigen Überlagerung $ \rvert S \rangle $.
Alle Achsen in dem $ 2^N $ dimensionalem Raum, und somit alle Kombinationen von 0en und 1en, haben den gleichen kleinen Anteil an $ \rvert S \rangle $. Da $ \rvert S \rangle $, wie jeder Zeiger auf der Kugeloberfläche in dem $ 2^N $ dimensionalen Raum, die Länge 1 hat, ist der Anteil von jedem Qubit-Zustand an $ \rvert S \rangle $ nur ein kleiner Bruchteil von 1. Zunächst würde man vermuten dieser Bruchteil wäre $ 1/2^N $, da es $ 2^N $ Kombinationen gibt. Dies ist aber nicht so: Aufgrund des Satzes von Pythagoras vii ist der kleine Bruchteil die Wurzel davon, und zwar $ 1/ \sqrt{2^N} $. Und somit zeigt der Zeiger der gleichmäßigen Überlagerung zu diesem kleinen Bruchteil auch in Richtung unseres Lösungszeigers $ \rvert 10001101100 \rangle $. Insbesondere wird dieser Bruchteil also schnell kleiner je größer N wird. Das Wurzelzeichen wird sich später übrigens als der Clou für den Grover-Algorithmus herausstellen!
Jetzt zum dritten Zeiger, den wir $ \rvert s \rangle $ nennen wollen: Der entsteht, wenn wir aus der gleichmäßigen Überlagerung $ \rvert S \rangle $ den kleinen $ \rvert 10001101100 \rangle $ – Anteil herausrechnen. $ \rvert s \rangle $ zeigt damit genau in X-Richtung. $ \rvert S \rangle $ und $ \rvert s \rangle $ liegen also nah beieinander. Der Winkel der sie trennt ist gerade $ 1/ \sqrt{2^N} $ viii. Das der Winkel zwischen $ \rvert S \rangle $ und $ \rvert s \rangle $ so klein ist, wird uns am Ende noch mächtig ärgern!
Wenn wir uns das Diagramm ansehen können wir erkennen, was der Grover-Algorithmus leisten muss:
Wir nennen den aktuellen Zustand des Quantencomputers einfach $ \rvert x \rangle $. Er wird normalerweise eine Überlagerung von verschiedenen anderen Zuständen sein. Am Anfang starten wir mit dem Zustand der gleichmäßigen Überlagerung, also $ \rvert x \rangle = \rvert S \rangle $. Wir müssen jetzt eine Reihe von Quantengattern derart zusammenschalten, dass $ \rvert x \rangle $ nach und nach in die Richtung unserer Lösung $ \rvert 10001101100 \rangle $ zur Y-Achse gedreht wird.
Im Folgenden erfahren Sie zunächst, was es mit dem Zeiger $ \rvert s \rangle $ auf sich hat.
Das Orakel: Eine einfache Spiegelung
Schauen wir uns an wie ein Quantengatter den Zustand der gleichmäßigen Überlagerung verändert. Dank des Superpositionsprinzip wissen wir: Ein Quantengatter verändert eine Überlagerung von Zuständen derart, dass wir danach eine Überlagerung von veränderten Zuständen haben: z.B.
$ X ( \rvert 0 \rangle – \rvert 1 \rangle ) = X \rvert 0 \rangle – X \rvert 1 \rangle = \rvert 1 \rangle – \rvert 0 \rangle $
Das gleiche gilt natürlich immer noch, wenn wir mehrere Quantengatter miteinander kombinieren. Das Orakel ist insbesondere auch einfach eine Zusammenschaltung von mehreren Quantengattern. Nennen wir es O.
O soll wie folgt die verschiedenen überlagerten Teilzustände verändern:
- Wenn eine Kombination von 0en und 1en keine Lösung des Problems ist, wir erinnern uns, dass wir dies für NP-Probleme leicht herausfinden können, bleibt dieser Anteil an der gesamten Überlagerung unverändert. Als Gleichung geschrieben:$ O \rvert 10101010101 \rangle = \rvert 10101010101 \rangle $
- Wenn eine Kombination von 0en und 1en eine Lösung ist, wird dieser Anteil an der gesamten Überlagerung ins Negative umgekehrt. Als Gleichung geschrieben:$ O \rvert 10001101100 \rangle = – \rvert 10001101100 \rangle $
Wenn wir uns das Zeigerbild ansehen, können wir jetzt Folgendes erkennen:
$ O $ verändert fast alle Anteile an dem Anfangszustand $ \rvert S \rangle $ nicht. Nur der Anteil in die Y-Richtung wird umgekehrt. Das ist aber nichts anderes als eine Spiegelung an der X-Achse, die ja der Zustand $ \rvert s \rangle $ ist.
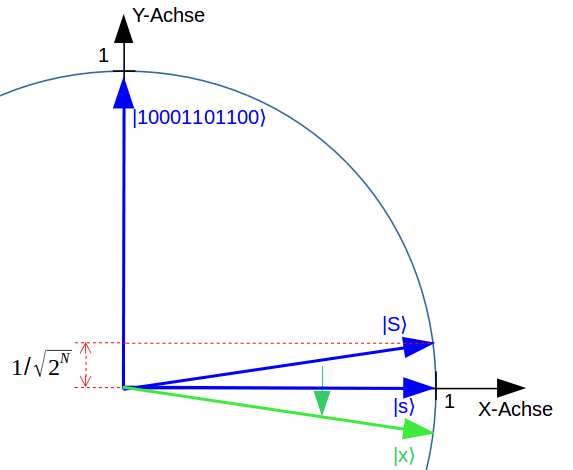
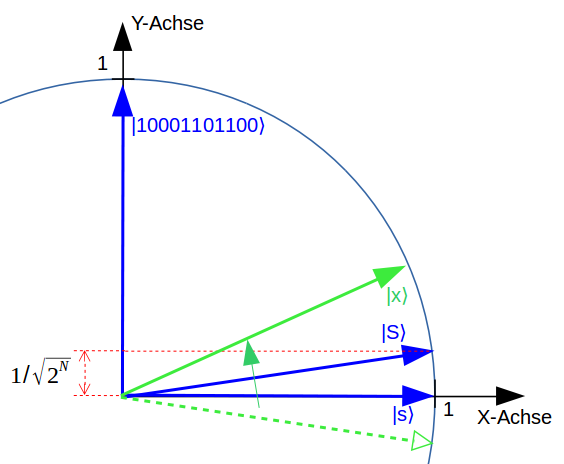
Zunächst haben wir dadurch nichts gewonnen, weil der Zeiger $ \rvert x \rangle $ sich noch nicht näher an $ \rvert 10001101100 \rangle $, unserer Y-Achse angenähert hat. Deshalb spiegeln wir $ \rvert x \rangle $ nochmal. Diesmal allerdings nicht an $ \rvert s \rangle $, sondern an $ \rvert S \rangle $!
Der aktuelle Zustand des Quantencomputers $ \rvert x \rangle $ ist um einen Winkel näher an die Y-Achse gedreht. Dieser zusätzliche Winkel ist das zweifache von dem kleinen Winkel zwischen $ \rvert S \rangle $ und $ \rvert s \rangle $, also $ 2 / \sqrt{2^N} $.
Zwischenfazit: Die Stärken und Schwächen des Grover-Algorithmus
Jetzt können wir erkennen, wie es weitergehen muss: Jedes mal wenn wir den aktuellen Zeiger $ \rvert x \rangle $ zuerst an $ \rvert s \rangle $ spiegeln und danach an $ \rvert S \rangle $, dreht sich $ \rvert x \rangle $ um den Winkel $ 2/ \sqrt{2^N} $ näher an $ \rvert 10001101100 \rangle $ heran.
Weil der Winkel leider so klein ist, müssen wir das Ganze ungefährt $ \frac{1}{2} * \sqrt{2^N} $ Mal durchführen.
Damit haben wir tatsächlich schon das Prinzip des Grover-Algorithmus gelöst und damit auch die Antwort auf unsere Brute Force / NP-Cruncher-Frage herausbekommen!
Ein herkömmlicher Computer würde im Schnitt $ \frac{1}{2} * 2^N $ Versuche brauchen, um $ 2^N $ Kombinationen durchzuprobieren und eine Lösung zu erhalten. Ein Quantencomputer braucht mit dem Grover-Algorithmus $ \frac{1}{2} * \sqrt{2^N} $ Versuche. Das ist eine quadratische Beschleunigung!
Wenn also ein herkömmlicher Computer für ein Brute-Force-Problem eine Millionen Rechenschritte benötigen würde, bräuchte ein Quantencomputer nur 1000 Rechenschritte. Das ist schon sehr gut!
Aber leider hatten wir uns mehr davon versprochen: Was stört, ist dass wir immer noch $ \sqrt{2^N}= 2^{\frac{1}{2}N} $ Rechenschritte benötigen. Das ist immer noch mehr als polynomial. Polynomialer Rechenaufwand wäre $ N^{\text{etwas}} $. Damit ist das Problem kein BQP-Problem und ein schwieriges NP-Problem bleibt also auch ein schwieriges Problem für den Grover-Algorithmus, obwohl letzterer es zumindest schneller lösen kann.
Die große Frage ist nun: Ginge das auch besser?
Was so sehr stört ist, dass der Winkel zwischen $ \rvert S \rangle $ und $ \rvert s \rangle $ so klein ist. Dies ist so etwas wie die Quantenversion der Tatsache, dass die gesuchte Kombination 10001101100 eine unter sehr sehr vielen Kombinationen ist. Vielleicht können wir den Grover-Algorithmus z.B. derart ändern, dass wir bei jeder Reflexion an $ \rvert s \rangle $ näher an $ \rvert 10001101100 \rangle $ herankommen.
Tatsächlich wurde eine Grenze für ein Optimum an Verbesserung für den Grover-Algorithmus gefunden. Jeder Algorithmus, der das Orakel $ O $ mehrmals verwendet sieht prinzipiell so aus:
$ … O … O … O … O … $
Die Pünktchen stehen jeweils für irgendeine Schaltung an Quantengattern. Es ist erstaunlich aber man kann tatsächlich prinzipiell beweisen, dass jeder Einsatz eines Orakels in dieser Form den Rest des Quanten-Algorithmus, also die Pünktchen, höchstens quadratisch beschleunigen kann ix. Das zeigt, dass der Grover-Algorithmus tatsächlich optimal ist. Leider.
Natürlich gibt es viele Quanten-Algorithmen, die die besten herkömmlichen Algorithmen exponentiell beschleunigen, wie z.B. der Shor-Algorithmus. Evtl. gibt es sogar doch noch einen ultimativen NP-Cruncher, der auf Quantencomputern mit Polynomialaufwand läuft. Aber die Idee, diesen NP-Cruncher dadurch zu konstruieren, indem man ein Orakel mehrmals hintereinander ausführt, führt leider nicht zum gewünschtem Ziel.
Der Grover-Algorithmus als Quanten-Schaltkreis
Achtung, jetzt wird es ernst!
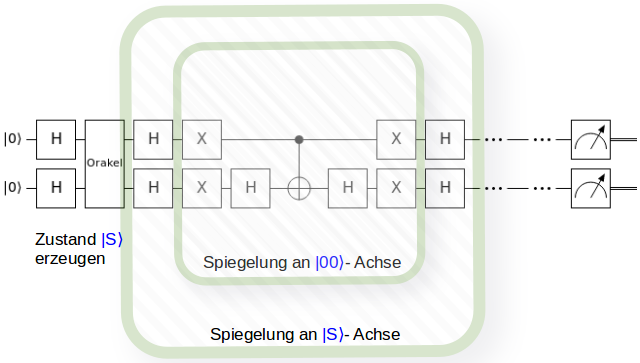
Bisher hatte ich den Grover-Algorithmus anhand der geometrischen Anschauung erklärt. Jetzt schauen wir uns den Quanten-Schaltkreis für den Grover-Algorithmus auf einem 2 Qubit – Quantencomputer an:
(In meinem Artikel „Quantencomputer programmieren“ stelle ich Ihnen dazu ein konkretes Quantenprogramm für IBMs Quantencomputer vor).
Am Anfang auf der linken Seite ist jedes Qubit im Zustand $ \rvert 0 \rangle $ vorhanden. Anders ausgedrückt: $ \rvert 00 \rangle $. Darauf erzeugen wir den Zustand der gleichmäßigen Überlagerung $ \rvert S \rangle $, in dem wir auf jedes Qubit das Hadamard-Quantengatter anwenden. Die beiden Qubits bilden jetzt eine Überlagerung aus allen möglichen Kombinationen von 0en und 1en.
Danach führen wir das Orakel aus. Das Orakel muss für jedes Problem individuell konstruiert werden, weil die Prüfroutine für Lösungskandidaten natürlich jeweils anders aussieht. Beispiele hierfür gebe ich weiter unten.
Im Gegensatz dazu sieht die Spiegelung an $ \rvert S \rangle $ für jedes Problem gleich aus. Zum Glück kann man sie einfach aus der Spiegelung an der $ \rvert 00 \rangle $ – Achse ableiten.
Letztere ist im inneren Kasten dargestellt:
Zunächst zum Quantengatter ganz in der Mitte. Dieses heißt „Controlled NOT“ bzw. CNOT. Das CNOT-Quantengatter ist so etwas wie eine „Wenn-Dann / If-Then“-Schaltung für Quantencomputer. Es arbeitet so: Falls das obere Qubit
- den Zustand |0⟩ hat, lässt es das untere Qubit unverändert
- den Zustand |1⟩ hat, tauscht es die Zustände |0⟩ und |1⟩ um unteren Qubit, führt also ein X – Quantengatter auf das untere Qubit aus.
Das obere Qubit „kontrolliert“ also den X-Tausch im unteren Qubit, deshalb der Name. Normalerweise sind beide Qubits überlagert. In dem Fall tauscht das obere Qubit den überlagerten Zustand des unteren Qubit „ein bißchen und ein bißchen nicht“. Dadurch entsteht so ein berühmt-berüchtigter verschränkter Quantenzustand: Die beiden Qubits sind jetzt so tiefgreifend miteinander verwoben, dass man sie nicht mehr als einzelne Einheiten betrachten kann, sondern nur als Ganzes.
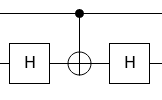
Für den inneren Kasten in unserem Grover-Schaltkreis ist das Entscheidende, dass man das CNOT-Quantengatter auch als Spiegelung auffassen kann. Das verwundert nicht, weil wir oben gesehen hatten, dass das X-Quantengatter unter anderem eine Spiegelung an der Achse $ H \rvert 0 \rangle $ ist. So richtig klar wird es, wenn wir diese Spiegelung auf die Achse des Zustands |11⟩ drehen. Das erreichen wir durch die Schaltung $ H CNOT H $ in der Mitte, was man übrigens auch „Controlled Z“ oder CZ nennt. Die CZ-Quantenschaltung arbeitet insgesamt so: Falls das obere Qubit
- den Zustand |0⟩ hat, lässt es das untere Qubit unverändert
- den Zustand |1⟩ hat, lässt es den |0⟩ – Anteil des unteren Qubits unverändert und kehrt den und |1⟩ – Anteil ins Negative um.
Oder als Gleichung:
CZ ( |00⟩ + |10⟩ + |01⟩ + |11⟩ ) = |00⟩ + |10⟩ + |01⟩ –|11⟩
Das ist aber tatsächlich nichts anderes als eine Spiegelung! Genauso hatten wir nämlich oben auch die Funktionsweise des Orakels erklärt. Jetzt überprüfen wir noch an welcher Achse hier gespiegelt wird. Eigentlich kehrt sich in der Gleichung der |11⟩ – Anteil ins Negative. Nun muss man wissen, dass ein Quantencomputer bei jeder Messung am Ende globale Minuszeichen eines Zustandes ignoriert. Es macht am Ende also keinen Unterschied, wenn wir die komplette Qubit-Überlagerung mit „-1“ mal nehmen:
|00⟩ + |10⟩ + |01⟩ –|11⟩ ist gleichwertig mit
– |00⟩ – |10⟩ – |01⟩+ |11⟩
Das macht die Controlled Z – Quantenschaltung also zu einer Spiegelung an der |11⟩ –Achse.
Schauen wir uns noch den Rest von dem inneren Kasten im Quanten-Schaltkreises oben an:
Die beiden unteren X – Quantengatter links und rechts von der Controlled Z – Schaltung $ H CNOT H $ drehen die Spiegelachse von der |11⟩-Achse zunächst auf die |10⟩-Achse. Die beiden oberen X-Quantengatter links und rechts drehen die Spiegelachse weiter auf die |00⟩-Achse.
Soweit zum inneren Kasten. Den Trick mit dem CZ – Quantengatter merken wir uns für später, wenn wir die Spiegelung für das Orakel konstruieren.
Die zusätzlichen Hadamard-Quantengatter im äußeren Kasten drehen dann die Spiegelachse $ \rvert 00 \rangle $ auf den Zustand $ \rvert S \rangle $, also ganz analog zu der Gleichung weiter oben $ H \rvert 00 \rangle = \rvert S \rangle $.
Alles verstanden?
Ich vermute, jetzt bekommen Sie langsam ein Ahnung, warum Quanten-Algorithmen so kompliziert sind. Und dabei ist der Grover-Algorithmus noch verhältnismäßig einfach 🙂 !
Die Pünktchen im weiteren Verlauf des Quanten-Schaltkreises deuten an, dass danach das Orakel und die Spiegelung an $ \rvert S \rangle $ entsprechend oft wiederholt werden müssen, damit der Lösungszustand verstärkt wird.
Am Ende erfolgt dann die Messung der einzelnen Qubits, die dann die gesuchte Lösung mit hoher Wahrscheinlichkeit ergibt.
Das Beispiel beschreibt den Fall für 2-Qubits. Für mehrere Qubits sieht die Schaltung prinzipiell genauso aus.
Ein Beispiel-Orakel für ein echtes „3SAT“-Problem
Eine der großen Stärken des Grover-Algorithmus ist es, dass er ein sehr universeller Algorithmus ist, den wir für eine riesige Auswahl an Problemen verwenden können. Der Teil des Quanten-Schaltkreises, den ich Ihnen im vorigen Abschnitt vorgestellt habe, sieht dabei für jedes Problem gleich aus. Der Teil des Quanten-Schaltkreises, der speziell für jedes Problem angepasst werden muss, ist das Orakel selbst.
Um einen Eindruck von einem Grover-Orakel zu bekommen, stelle ich Ihnen zwei Beispiele vor.
- Das erste Grover-Orakel gehört zu einem Problem, das so simpel ist, dass ich es „Deppen-Problem“ nenne.
- Das zweite Grover-Orakel ist wesentlich interessanter und auch wesentlich komplexer. Es gehört zu den sogenannten „3SAT“-Problemen, die zu den universellen NP-Complete-Problemen zählen. Aber dazu gleich mehr.
Kommen wir erstmal zum „Deppen-Orakel “:
Es ist leider das Standardbeispiel für ein Grover-Orakel und geistert in vielen Einführungen für den Grover-Algorithmus herum. Es ist so einfach, dass man nicht versteht worin überhaupt das Problem besteht.
In dem „Deppen-Problem“ werden die zwei Bits gesucht, also zwei Zahlen mit Werten 0 oder 1, die folgende Gleichungen erfüllen:
$ X_1 $ = 1
$ X_2 $ = 1
Dieses Problem liefert also seine eigene Lösung gleich mit! Es ist so einfach, dass man den ganzen Sinn und Zweck des Orakels im Grover-Algorithmus nicht richtig verstehen kann. Für den Einstieg zeige ich Ihnen trotzdem auch den Quanten-Schaltkreis zu diesem Orakel.
Nochmal zur Erinnerung: Wie muss das Orakel O in dem Grover-Algorithmus funktionieren? Das hatte ich oben beschrieben.
O soll wie folgtdie verschiedenen überlagerten Teilzustände von $ O \rvert x\rangle $ verändern:
- Für alle Kombinationen von 0en und 1en, die keine Lösung sind (also |x⟩ = |00⟩, |01⟩ und |10⟩) bleibt der Anteil an der gesamten Überlagerung unverändert. Als Gleichung geschrieben:$ O \rvert x \rangle = \rvert x \rangle $
- Nur der |11⟩er- Anteil an der gesamten Überlagerung wird ins Negative umgekehrt. Als Gleichung geschrieben:$ O \rvert 11 \rangle = – \rvert 11 \rangle $
Diesen Schaltkreis kennen wir bereits. Es ist gerade die Controlled Z – Quantenschaltung oder CZ, die wir oben kennen gelernt hatten:
Der ganze Grover-Schaltkreis sieht damit so aus:

Kommen wir aber jetzt zu einem vernünftigen Beispiel: Ein 3SAT-Problem.
Zunächst zu den SAT-Problemen bzw. den „Boolean Statisfiability“-Problemen:
So werden in der Informatik Systeme von Gleichungen mit mehreren Bit-Zahlen genannt. Dabei können die Bit-Zahlen jeweils mit UND, ODER oder NICHT miteinander verknüpft werden. Unser „Deppen-Problem“ ist also auch ein sehr einfaches SAT-Problem. 3SAT-Probleme wiederum sind solche SAT-Probleme, bei denen in jeder Bit-Gleichung nur drei Bit-Zahlen vorkommen dürfen. Zum Beispiel
$ (NICHT \ x_1) \quad ODER \quad (NICHT \ x_3) \quad ODER \quad (NICHT \ x_4) = 1 $
$ x_2 \quad ODER \quad x_3 \quad (NICHT \ x_4) = 1 $
$ x_1 \quad ODER \quad (NICHT \ x_2) \quad ODER \quad x_4 = 1 $
$ (NICHT \ x_1) \quad ODER \quad X_2 \quad ODER \quad (NICHT \ x_4) = 1 $
Sie werden mir zustimmen, das Problem sieht schon schwieriger aus! Die Komplexität von 3SAT-Problemen ist sogar amtlich: Sie gehören zu den „NP-Complete“-Problemen: Alle NP-Probleme können in 3SAT-Probleme umgewandelt werden. Könnte man alle 3SAT-Probleme einfach lösen, so könnte man auch man also alle NP-Probleme einfach lösen x.
Das 3SAT-Orakel, das ich Ihnen hier vorstelle stammt übrigens von Craig Gidney xi, dem Urheber des öffentlichen Quantencomputer-Simulators „Quirk“, mit dem ich die Quanten-Schaltkreise auf „quantencomputer-info.de“ erstelle. Mittlerweile ist er Mitarbeiter in Googles Quantum AI Lab und hat dort u.a. federführend die Programmierschnittstelle „Cirq“ mitentwickelt.
Gidney gibt folgenden Tipp, um ein Grover-Orakel zu konstruieren: Überlege Dir zu dem Problem den klassischen Schaltkreis für herkömmlichen Computer. Dann wandel die klassischen Gatter in Quantengatter um.
Unsere vier Gleichungen oben können wir umschreiben in eine Gleichung, die wir zu einem Schaltkreis umwandeln können. Da für Quantencomputer UND-Verknüpfungen handlicher sind als Oder-Verknüpfungen, müssen wir die Gleichungen noch zusätzlich umwandeln. Dabei machen wir uns zunutze, dass z.B. gilt $ (NICHT \ x_1) \quad ODER \quad (NICHT \ x_3) = NICHT( x_1 \quad UND \quad x_3) $.
$ NICHT \big( \quad x_1 \quad UND \quad x_3 \quad UND \quad x_4 \quad \big) \quad UND $
$ NICHT \big( \quad (NICHT \ x_2) \quad UND \quad (NICHT \ x_3) \quad UND \quad x_4 \big) \quad UND $
$ NICHT \big( \quad (NICHT \ x_1) \quad UND \quad x_2 \quad UND \quad (NICHT \ x_4) \big) \quad UND $
$ NICHT \big( \quad x_1 \quad UND \quad (NICHT \ x_2) \quad UND \quad x_4 \big) \quad UND $
$ = 1 $
Danach schreiben wir die Gleichungen als Tabelle um und zwar in derselben gedrehten Sichtweise, wie auch unser Quanten-Schaltkreis ausgerichtet sein wird.
|
Gleichung 1 |
Gleichung 2 |
Gleichung 3 |
Gleichung 4 |
|
|
Bit 1 |
Bit1 |
NICHT Bit1 |
Bit1 |
|
|
Bit 2 |
NICHT Bit 2 |
Bit2 |
NICHT Bit2 |
|
|
Bit 3 |
Bit3 |
NICHT Bit3 |
Bit3 |
|
|
Bit 4 |
Bit4 |
Bit4 |
NICHT Bit4 |
Der Quanten-Schaltkreis dazu ist unten dargestellt. Darin verwenden wir für jedes Bit natürlich ein Qubit. Jede Gleichung wird durch ein mehrfaches UND-Quantengatter dargestellt. Die schwarzen Kreise bedeuten, dass das Qubit so wie es ist UND-verknüpft wird. Die weißen Kreise bedeuten, dass das Qubit vor der UND-Verknüpfung mit einem X-Gatter NICHT-verknüpft wird. Das Ergebnis jeder Gleichung wird in einem zusätzlichen „Ancilla“-Qubit hinterlegt. Am Ende werden alle diese Ancilla-Qubits mit einem mehrfachen NICHT-UND-Gatter verknüpft, genauso wie es unser 3SAT-Problem verlangt. Das Endergebnis hinterlegen wir in einem zusätzlichen Qubit. Immer wenn dieses Qubit den Zustand |1⟩ besitzt, sind alle unsere Gleichungen erfüllt. In allen anderen Fällen ist das letzte Qubit im Zustand |0⟩.
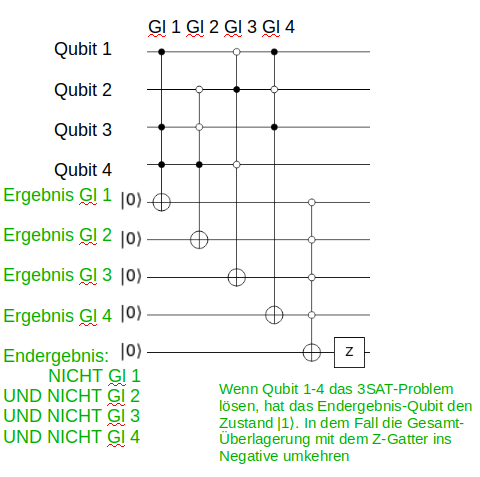
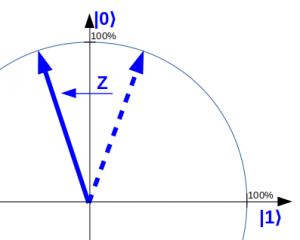
Am Ende müssen wir uns noch um unser Orakel kümmern: Immer wenn eine Bit-Kombination alle Gleichungen erfüllt, soll sich der Teil der Überlagerung ins Negative umkehren und ansonsten so bleiben wie er ist. Oder anders ausgedrückt, immer wenn das Qubit für das Endergebnis im Zustand |1⟩ ist, soll sich der Teil an der Gesamt-Überlagerung |x⟩ ins Negative umkehren. Wenn das Endergebnis-Qubit im Zustand |0⟩ ist, soll der Teil der Gesamt-Überlagerung |x⟩ so bleiben wie er ist. Das Quantengatter, das sich genauso verhält, nennt man Z-Quantengatter.
Z |0⟩ = |0⟩ und Z |1⟩ = – |1⟩
In unserem vereinfachten Zeigerbild für Qubits ist das eine Spiegelung an der |0⟩ – Achse:
Die Schaltung oben ist allerdings wieder eine starke Vereinfachung. Für jede der 4 Bit-Gleichungen habe ich nur ein Quantengatter dargestellt. Tatsächlich müssten wir es jeweils mit einer Vielzahl zusätzlicher CNOT- und weitere Quantengatter ersetzen. Aber das ist tatsächlich „nur“ noch eine Fleißarbeit xii.
Fußnoten
i Polynomialer Rechenaufwand bedeutet Folgendes: Je komplexer das Problem wird, desto mehr nimmt natürlich die Zeit zu um die Lösung zu finden. Polynomialer Rechenaufwand bedeutet nun, dass die Anzahl der Rechenschritte um die Lösung zu finden nach einer Potenzregel zunimmt. Wenn N die Komplexität des Problems ist, so nimmt der Rechenaufwand dann grob gesehen wie N oder N² oder N³ oder N⁴, …. zu. Um z.B. eine Person unter N=1000 Personen zu finden, benötigt man im Mittel ½ * N Versuche. Probleme bei denen der Aufwand mehr als polynomial zunimmt, wären etwa Probleme deren Lösungsaufwand explosionsartig bzw. exponentiell zunimmt z.b. $ 2^N $. Solche Probleme sind eher charakteristisch für NP-Probleme.
ii Eine sehr schöne Einführung in die Komplexitätstheorie bekommen Sie auf Scott Aaronsons Website zu seinem Buch „Quantum Computing Since Democritus“: https://www.scottaaronson.com/democritus/lec6.html. Scott Aaronson ist einer der führenden Quanteninformatiker und ein fesselnder Didakt.
iii Mathematische Beweise sind insbesondere auch Kandidaten für NP-Probleme. Einen fertigen Beweis zu verifizieren ist, zumindest für Fachleute, gut machbar. Die Kunst ist es einen Beweis für ein Problem zu finden. So formulierte beispielsweise Pierre de Fermat seine berühmte Vermutung an + bn = cn in den 1650er Jahren. Trotz intensivsten Bemühungen von führenden Mathematikern wurde der Beweis hierfür erst 1994 von Andrew Wiles mithilfe von modernsten Methoden der arithmetischen Geometrie gefunden.
iv Tatsächlich ist das Diagramm über die Zusammenhänge zwischen P, NP, BQP und PSPACE fast komplett unbewiesen. Wirklich bewiesen wurde zuletzt allerdings die Vermutung, dass es BQP-Probleme gibt, die weder in P noch in NP liegen. Nebenbei wurde damit auch bewiesen, dass PSPACE und NP nicht gleich sind. Lesen Sie hierzu auch den Artikel auf Quantamagazine https://www.quantamagazine.org/finally-a-problem-that-only-quantum-computers-will-ever-be-able-to-solve-20180621/
v Der Begriff „Orakel“ hat für die Computerwissenschaften eine noch speziellere Bedeutung, was für den Grover-Algorithmus aber nicht wichtig ist.
vi Das exakte Bild eines Qubits ist das einer Kugeloberfläche. Die Zustände |0⟩ und |1⟩ müssen wir dann an Nord- und Südpol einzeichnen. Um von der Kreislinie zur Kugeloberfläche zu gelangen, muss ein zusätzliche Winkel verwendet werden, der auch „Phase“ genannt wird.
vii Zur Erinnerung: $ \sqrt{ a^2 + b^2 } = c $, wenn $ a $ und $ b $ senkrecht aufeinander stehen. Wenn jetzt noch mehr senkrechte Achsen dazukommen, erhalten wir $ \sqrt{ a_1^2 + a_2^2 + a_3^2 + a_4^2 + …} = c $. Da die $ 2^N $ $ a $‘s in der gleichmäßigen Überlagerung alle gleich lang sind und $ c $ die Länge 1 hat, bekommen wir $ \sqrt{ 2^N a^2 } = 1 $ was gerade $ a = 1 / \sqrt{2^N} $ ist
viii Da wir die Winkel als Radianten bzw. Kreisbogen messen, müssen wir genau genommen vor alle Winkel noch einen Faktor $ \pi / 2 $ schreiben. Um das ganze Thema nicht noch komplizierter aussehen zu lassen und uns nur das grobe Verhalten des Grover-Algorithmus interessiert, können wir diesen auch weglassen.
ix https://arxiv.org/abs/quant-ph/9701001: Fachartikel „Strengths and Weaknesses of Quantum Computing“. Eine besser verdauliche Variante des Beweises findet man in dem Standard-Lehrbuch „Quantum Computation and Quantum Information“ von Michael Nielsen und Isaac Chuang, oft auch kurz „Mike and Ike“ genannt.
x https://www.scottaaronson.com/democritus/lec6.html: „PHYS771 Lecture 6: P, NP, and Friends“, die 6. Vorlesung aus Scott Aaronson‘s legendären Vorlesungsreihe „Quantum Computing Since Democritus“. Darin beleuchtet Aaronson, einer bekanntesten Theoretiker für Quantencomputer weltweit, viele Grundlagen-Aspekte aus Mathematik, Informatik und Quantenmechanik auf eine erfrischend mitreißende Weise.
xi https://cstheory.stackexchange.com/questions/38538/oracle-construction-for-grovers-algorithm/38551#38551: „Oracle Construction for Grover’s Algorithm“, Thread auf CSTheory- Stackexchange
xii Die Quantengatter für jede Gleichung sind abgewandelte CCCNOT-Schaltungen. Teilweise müssten hier noch X-Gatter für die NICHT-Verknüpfungen in den Gleichungen vorgeschaltet werden. CCCNOT-Schaltungen können über mehrere CCNOT-Schaltungen erstellt werden: https://quantumcomputing.stackexchange.com/questions/2397/implementing-a-cccnot-gate-using-only-toffoli-gates. CCNOT-Gatter wiederum sind die Quantencomputer-Version von klassischen UND-Gattern und werden oft auch Toffoli-Gatter genannt. Ein Toffoli-Gatter kann wiederum über 6 CNOT-Gatter konstruiert werden: https://en.wikipedia.org/wiki/Toffoli_gate
