Autor: Jens Marre

<<   >>

Künstliche Intelligenz und Machine Learning mit Quantencomputern: Nur ein Superhype?

Künstliche Intelligenz und Machine Learning sind in aller Munde. Unser Alltag wird immer mehr durch sie bestimmt, sowohl im Offensichtlichen als auch im Verborgenen. Viele Branchen können sich gar nicht mehr erlauben Investitionen in Künstliche Intelligenz und Machine Learning zu ignorien. Staaten treiben mit Milliarden an Fördergeldern die Erprobung neuer Möglichkeiten voran ⁱ, und große gesellschaftliche Umbrüche stehen uns bevor.

Mit anderen Worten: Künstliche Intelligenz und Machine Learning ist vielleicht das Hype-Thema unserer Tage schlechthin.

Einer anderen Technologie, die ein gewaltiges Potential hat, habe ich diese Webseite gewidmet: Den Quantencomputern.

Was passiert also wenn ein Hype auf einen anderen Hype trifft?

Vorsichtig sein, sagt uns unser Instinkt. In diesem Artikel gebe ich Ihnen einen realistischen und aktuellen Lagebericht zu dem Thema. Wie angebracht diese Vorsicht ist, beweist die folgende Episode.

Eine Teenagerin schreckt die komplette Forschergemeinde auf (Teil 1)

Juni 2018, University of California in Berkeley: Eine Woche lang beraten führende Wissenschaflter für Quantencomputer-Algorithmen auf der Konferenz „Challenges in Quantum Computation“ über die Herausforderungen vor denen die aktuelle Forschung steht.

Am Ende der Konferenz bittet Scott Aaronson, von der University of Texas in Austin und einer der führenden Köpfe der Quantencomputer-Szene, einige Teilnehmer zu einer Extraschicht in einer dringenden Angelegenheit. Die Forscher treffen sich in der Folgewoche wieder. Unter ihnen sind auch Iordanis Kerenidis und Anupam Prakash.

Zwei Jahre zuvor hatten die beiden Forscher einen Algorithmus für ein Quanten-Empfehlungssystem entwickelt ⁱⁱ. Empfehlungssysteme ermitteln Vorlieben von Kunden anhand ihrer Bestellhistorie und bilden häufig das Herzstück von Bigdata-Unternehmen wie Amazon oder Netflix.

Der neue Algorithmus von Kerenidis und Prakash hatte in der Zwischenzeit eine enorme Aufmerksamkeit in der Forschergemeinde bekommen. Er war einer der ersten Quanten-Algorithmen, der speziell auf eine reale Anwendung im Bereich Bigdata und Machine Learning zugeschnitten war und erwiesenermaßen eine exponentielle Beschleunigung gegenüber allen bekannten Algorithmen für herkömmliche Computer besaß.

Am Morgen des 18. Junis tritt Aaronsons junge Studentin Ewin Tang vor die erlesene Runde und beginnt einen Vortrag über Kerenidis und Prakashs Arbeit.

Und langsam dämmert den verblüfften Anwesenden die bittere Tragweite von Ewin Tangs Ausführungen … (Teil 2 folgt weiter unten).

Künstliche Intelligenz und Machine Learning: Ein Kurzüberblick

Um die Episode zu beenden und überhaupt um diesen Artikel zu verstehen, müssen wir erst mal ganz von vorne anfangen. Was ist eigentlich Künstliche Intelligenz oder Machine Learning?

Eines der Hauptziele der klassischen künstlichen Intelligenz und des Machine Learnings ist es Daten zu struktieren und zu klassifizieren. Folgende Schwerpunkte gibt es dabei:

• Supervised Machine Learning, überwachtes Maschinelles Lernen: Dabei werden bekannte und bereits beurteilte Daten dafür verwendet, um neue Daten zu klassifizieren. Das Standardbeispiel hierfür sind die Deep Learning – Netzwerke. Ein Deep Learning – Netzwerk wird z.B. mit beurteilten Tierbildern gefüttert (Bild 1 = „Katze“, Bild 2 = „Vogel“, Bild 3 = „Katze“, …). Nach einer längeren Anlernphase ist das Netzwerk optimiert bzw. trainiert und in der Lage neue, unbekannte Bilder richtig einzuordnen.
• Unsupervised Machine Learning, unüberwachtes Maschinelles Lernen: Dabei wird nach Zusammenhängen und Gruppen in Rohdaten gesucht, ohne dass irgendwelche Zusatzinformationen zu diesen Daten bekannt wären. Dadurch wird versucht, die Rohdaten auf das „Wesentliche“ zu reduzieren.
• Semi-supervised Machine Learning, teilüberwachtes Maschinelles Lernen: In einer Datenmenge sind einige Daten bereits beurteilt und einige noch nicht. Anhand der zusätzlichen Informationen wird versucht, die gesamte Datenmenge besser zu strukturieren und zu gruppieren. Dies geschieht insbesondere über statistische Methoden.

• Reinforced Machine Learning, bestärkendes Maschinelle Lernen: Das Verhalten eines Softwareagenten wird mittels „Belohnung und Bestrafung“ immer weiter verbessert.

Die ersten beiden Schwerpunkte erläutere ich Ihnen im Weiteren etwas genauer. Dabei stelle Ihnen einige Algorithmen für Quantencomputer vor, von denen man sich eine Beschleunigung gegenüber Methoden für herkömmliche Computer erhofft.

Wie Machine Learning – Algorithmen Rohdaten sehen

Um Rohdaten für das Machine Learning aufzubereiten, hat es sich bewährt, diese Daten als Zeiger bzw. „Vektoren“ in riesigen, hochdimensionalen Datenräumen darzustellen. Und mit „riesig“ meine ich jetzt nicht so etwas, wie die „grenzenlosen Weiten des Weltalls“, sondern einen abstrakten Hyperraum mit vielen, vielen Dimensionen (also Achsen, die jeweils senkrecht aufeinander stehen). Hier wieder mein Hinweis: Versuchen Sie erst gar nicht, sich mehr als drei senkrechte Achsen räumlich vorzustellen (nämlich Höhe, Länge, Breite). Wir Menschen können es einfach nicht! Die Mathematik hat damit allerdings überhaupt keine Probleme. Sie kann mit beliebig vielen Dimensionen arbeiten, sogar mit unendlich vielen.

Ein Bild mit 16 * 16 Pixeln, wird so z.B. als ein Zeiger in einem Datenraum mit 16 * 16 = 256 Dimensionen dargestellt. Falls Pixel Nr. 194 in dem Bild auch nur etwas grau ist, dreht sich der Datenzeiger etwas in die Richtung der 194. Achse und zwar umso mehr, je schwarzer der Punkt im Bild ist.

Machine Learning mit Quantencomputern

Solche Datenräume stellen für herkömmliche Computer einen gewissen Aufwand dar: Um z.B. einen Zeiger in einer Ebene mit auch nur zwei Dimensionen (also wie ein Uhrzeiger) mit einer Genauigkeit von 0.1% darzustellen, braucht Ihr Computer etwa 20 Bits. Um diesen Zeiger zu verändern, in dem er z.B. gedreht wird, muss auf jedes dieser 20 Bits ein größere Anzahl an elementaren Bit-Operationen ausgeführt werden.

Ein Quantencomputer besitzt solche Zeigerdarstellungen von Natur aus. In meinem Artikel „Das Qubit und ein Magier bei Britain has Got Talent“ erkläre ich Ihnen, dass sich ein Qubit selbst, etwas vereinfacht, wie ein Zeiger in einer Ebene verhält. Die Achsen heißen in dem Fall „0“ und „1“. Im Prinzip kann unser Zeiger-Beispiel also mit einem einzigen Qubit dargestellt werden.

Zeiger-Operationen sind prinzipiell ebenfalls direkt im Quantencomputer eingebaut und erfordern nur wenige Qubit-Operationen bzw. Quantengatter.

Aber es geht noch viel besser: Dieser Vorteil eines Quantencomputers verstärkt sich prinzipiell, je größer bzw. hochdimensionaler die Datenräume werden.

Und zwar exponentiell, also quasi explosionsartig!

Der Grund dafür ist, dass ein Quantencomputer seine potentielle Leistungsfähigkeit mit jedem weiteren Qubit verdoppelt. Dieses Quanten-Phänomen beschreibe ich genauer in meinem Einführungsartikel „Quantencomputer einfach erklärt“.

Unsupervised Machine Learning mit Quantencomputern

Dieser exponentielle Quanten-Vorteil ist bereits ein Hauptargument vieler Quanten-Algorithmen für Machine Learning.

Auch klassische Algorithmen können viele Information über Rohdaten ermitteln, wenn sie als Zeiger in einem Datenraum dargestellt werden. Über die bloße „räumliche“ Verteilung ihrer Zeigerspitzen in dem riesigen Datenraum können sie z.B. zu Gruppen zusammengefasst werden.

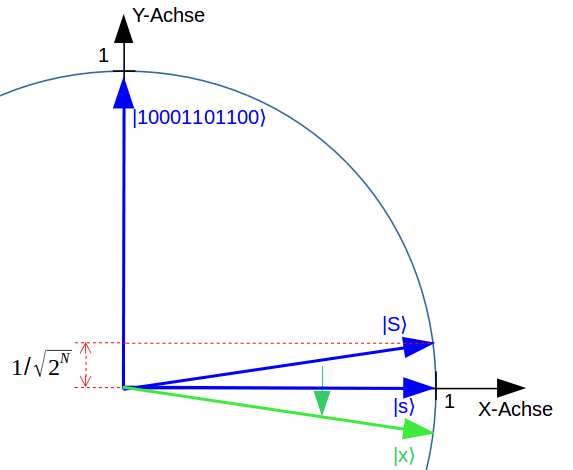
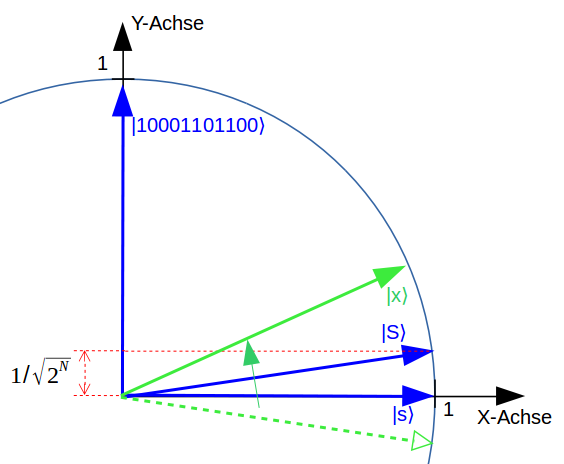
Ein Quantencomputer rechnet prinzipiell anders als ein herkömmlicher Computer. Abstände von zwei Zeigerspitzen können über einen kleinen Rechen-Trick allerdings auch mit einem Quantencomputer berechnet werden: Dabei werden die Zeiger in zwei neue, sehr spezielle Zeiger umgewandelt. Der Abstand der ursprünglichen Zeigerspitzen wird dann aus dem Winkel der zwei neuen Zeiger ermittelt ⁱⁱⁱ.

Die Hauptkomponentenanalyse mit Quantencomputern

Ein weiterer interessanter Algorithmus für das klassische Unsupervised Machine Learning ist die Hauptkomponentenanalyse bzw. Principal Component Analysis (PCA) ^iv. Die PCA verwendet für die Rohdaten ebenfalls den Datenraum. Darin werden die Datenpunkte bzw. die Zeigerspitzen als Bausteine eines massiven, starren Körpers interpretiert. Für diesen Körper können dann „mechanische Eigenschaften“ ermittelt werden. Die Hauptdrehachsen des Körpers (bei einem Spielzeugkreisel wäre die Hauptachse z.B. die senkrechte Drehachse des Kreisels) sind dann gerade die Hauptkomponenten des Datensatzes. Die PCA reduziert den starren Köper des Datensatzes im Prinzip auf einfachere geometrische Formen, mit ähnlichen mechanischen Eigenschaften. Die Rohdaten werden dadurch ebenfalls auf ihre Hauptkomponenten-Anteile reduziert.

Für die PCA wurde ebenfalls ein Quanten-Algorithmus mit einer exponentiellen Beschleunigung gefunden ^v. Dieser nutzt eine ganzen Latte von weiteren vielversprechenden Quanten-Algorithmen aus. Unter anderem der „Quantum Matrix Inversion“ oder geläufiger als „HHL-Algorithmus“ bezeichnet (nach seinen Autoren Harrow-Hassidim-Lloyd) ^vi. Der HHL-Algorithmus wurde 2008 gefunden und basiert selbst auf mehreren Algorithmen, die ich auf quantencomputer-info.de teilweise schon vorgestellt habe. Er ist in der Lage sogenannte lineare Gleichungssysteme exponentiell schneller zu lösen als alle herkömmlichen Algorithmen. Solche Gleichungssysteme so extrem häufig, dass der HHL-Algorithmus mittlerweile einer der Eckpfeiler der Forschung für Quanten-Algorithmen ist.

Quantencomputer und Machine Learning: Lese das Kleingedruckte …

Die spektakulären Quanten-Algorithmen, die ich bisher erwähnt habe, haben allerdings mindestens einen ganz gewaltigen Haken: Wie kommen die klassischen Rohdaten in den Quantencomputer?

Ein Quantencomputer ist in der Lage die Rohdaten exponentiell effizient darzustellen, soweit korrekt. Trotzdem müssen sie aber erstmal irgendwie in den Quantencomputer gelangen. Wenn das nicht mindestens genauso effizient erfolgen kann, ist der ganze Vorteil des superschnellen Quanten-Algorithmus bereits ganz am Anfang wieder hinfällig.

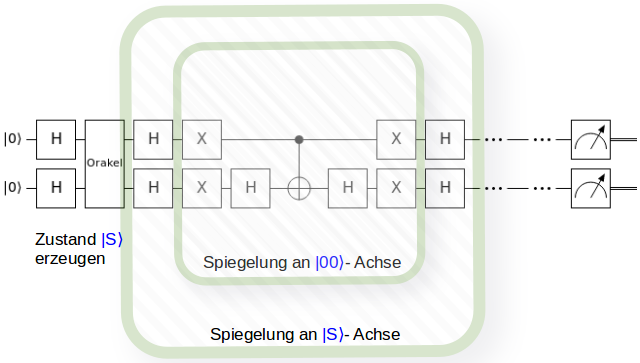
Wie dies erfolgen könnte wurde natürlich auch schon untersucht. Das vielversprechendste Konzept dafür nennt sich Quantum Random Access (QRAM) ^vii. QRAM hat aber auch einen Haken: Es gibt ihn noch nicht und wäre auch eine zusätzliche Quanten-Hardware, um die man sich kümmern müsste. QRAM besitzt eine Baumstruktur, an deren Knoten bzw. Verästlungen Quantenweichen sitzen, die jede Laderoutinen entweder in den linken oder in den rechten Seitenast weiterleiten. An den Blättern des Baumes befinden sich dann Informationen über die Zeiger der Rohdaten. Die Quantenweichen besitzen, anders als die Qubits, nicht zwei Quantenzustände, sondern drei. Von diesen Zuständen muss der Grundzustand besonders stabil sein. Die Entwicklung von QRAM ist noch völlig offen.

Ein weiterer Haken vieler Quanten-Algorithmen für Machine Learning: Wie Sie erfahren haben, basieren sie auf einer Mehrzahl zusätzlicher grundlegender Quanten-Algorithmen. Obwohl diese sehr spannend sind und großes Potential besitzen, wie z.B. der HHL-Algorithmus: Sie alle setzen die ein oder andere Bedingung voraus. Z.B. benötigen sie sehr große Quantencomputer oder eine gewisse Datenstruktur oder halt QRAM.

In Summe zu viele Fragezeichen für den eingangs erwähnten Scott Aaronson von der University of Texas. 2015 schrieb er einen Weckruf an seine Forscher-Kollegen: „Quantum Machine Learning Algorithms: Read the Fine Print“ ^viii und erhielt damit viel Zuspruch.

Eine Teenagerin schreckt die komplette Forschergemeinde auf (Teil 2)

Hier kommt seine junge Studentin wieder ins Spiel:

Ein Jahr später veröffentlichten Iordanis Kerenidis und Anupam Prakash den eingangs erwähnten Algorithmus für ein Quanten-Empfehlungssystem. Er war vielleicht der erste Algorithmus, der viele dieser Einschränkungen berücksichtigte, für eine reale Anwendung im Bereich Bigdata und Machine Learning zugeschnitten war und eine exponentielle Beschleunigung gegenüber allen bekannten Algorithmen für herkömmliche Computer besaß.

Was noch fehlte, war der Nachweis, dass es tatsächlich keinen schnelleren klassischen Algorithmus geben konnte. Scott Aaronson war genau davon überzeugt. Im Herbst 2017 übergab er die Suche nach diesem Nachweis an seine außerordentlich talentierte und vielversprechende Studentin Ewin Tang, als Thema für ihre Bachelor-Arbeit.

Was Ewin Tang dann der verblüfften Gruppe namhafter Forscher im Juni 2018 auf der Konferenz „Challenges in Quantum Computation“ in Berkeley präsentierte, war der von niemanden für möglich gehaltene Negativ-Nachweis. Ein neuer superschneller Algorithmus für Empfehlungssysteme sehr ähnlich wie der Quanten-Algorithmus Kerenidis und Prakash: Aber für herkömmliche Computer!

Erst später informierte Tangs Mentor Scott Aaronson die Forschern über ein weiteres kleines aber interessantes Detail zu dieser Entdeckung: Zum Zeitpunkt ihres Vortrages war Ewin Tang gerade einmal 18 Jahre alt ^ix.

„Quantum-inspired …“: Neue klassische Algorithmen für Machine Learning

Seit ihrer Entdeckung hat Ewin Tang eine Reihe von Artikeln über klassische Algorithmen mit dem Etikett „Quantum-inspired … “ veröffentlicht ^x. Diese machen die bereits gefunden Quanten-Algorithmen zwar nicht hinfällig, schränken aber wohl ihren Nutzen noch weiter ein ^xi.

Dabei ist Tangs Hauptargument das Folgende:

Wie viele andere Quanten-Algorithmen für Machine Learning und Linearer Algebra, geht auch der Algorithmus für das Quanten-Empfehlungssystem davon aus, dass die Datengrundlage (die Matrix von Benutzern und deren bekannten Produktvorlieben) Quantencomputer-gerecht und supereffizient in z.B. einer QRAM-Struktur abgelegt ist.

Tang argumentiert nun: Wer in der Lage ist, die Rohdaten in einer so aufwendigen Struktur von Quantenüberlagerungen abzulegen, sollte erst recht in der Lage sein, die Rohdaten in einer klassischen „Sample-And-Query“-Struktur abzulegen. Diese Struktur ist Tangs Pendant zum QRAM, ihm sehr ähnlich und genauso effizient aufgebaut. Anstatt mit Quanten-Überlagerungen arbeitet diese Datenbank mit reiner Statistik.

Die Rohdaten werden dabei in Datenfragmente aufgeteilt. Diese Fragmente werden in der SQ-Struktur nach ihrer Signifikanz am kompletten Datensatz statistisch gewichtet und können von dort supereffizient abgerufen werden. Die komplexe Berechnung des Quanten-Empfehlungssystems ersetzt Tang durch eine clevere statistische Einzelrechnung mit zufällig ausgewählten Datenfragmenten gemäß ihrer Gewichtung. Da auch die statistische Signifikanz der Fragmente abgerufen werden kann (ihre „statistische Verteilung“), ist Tang in der Lage das gesuchte, exakte Endergbnis abzuschätzen: Als Mittelwert aus der Statistik dieser Einzelergebnisse und mit jedem zusätzlichen Einzelergebnis immer genauer.

Dank des Quanten-Parallelismus kann der Quanten-Algorithmus von Kerenidis und Prakash von Anfang an mit dem kompletten Datensatz und exakt rechnen. Die Messung des Endergebnisses ist dann allerdings von der Quanten-Statistik abhängig. Im Gegensatz dazu „mißt“ Tang also nur Fragmente der Rohdaten gemäß ihrer statistischen Signifikanz und das schon ganz am Anfang. Dadurch reduziert sie die Datengröße und somit den Rechenumfang exponentiell und komponsiert den fehlenden Quanten-Parallelismus.

Wer meint, dass sich jetzt so ziemlich jedes Bigdata-Unternehmen um Ewin Tangs – Algorithmen reißen müsste, wird etwas enttäuscht. Tang bewertet den Nutzen ihrer bisherigen Arbeit für reale Anwendungsfälle in ihrem Blog nur „verhalten positiv“ ^xii.

Trotz des „Negativ-Ergebnisses“ zeigt diese Episode auch, wie fruchtbar die neuen Denkansätze für Quantencomputer selbst für herkömmliche Computer sein können. Oder wie Matthias Troyer von Microsoft Research es formuliert hat: „Ein Quanten-Algorithmus für Null Qubits“.

Quantencomputer, Künstliche Intelligenz und Machine Learning: Die Suche nach neuen Algorithmen

Als Zwischenfazit können wir festhalten: Die Quantencomputer-Forschung hat für die Künstliche Intelligenz und für das Machine Learning bereits eine Reihe interessanter Algorithmen entwickelt, die aber ihren Geschwindigkeitsvorteil hauptsächlich aus Unterroutinen wie QRAM und dem HHL-Algorithmus beziehen.

Wann und ob diese überhaupt eingesetzt werden können, ist noch offen.

Erst vor ein paar Jahren hat man damit begonnen, nach ganz neuen Wegen für die Künstliche Intelligenz und für das Machine Learning mit Quantencomputern zu suchen. Und zwar nach solchen Wegen, die bereits mit den kommenden Generationen von Quantencomputer beschritten werden können. Für Letztere prägte der bekannte Quantencomputer-Forscher John Preskill den Begriff „Noisy Intermediate Scale Quantun Computers“ (NISQ): Fehleranfällige, mäßig skalierte Quantencomputer ^xiii.

Drei prominente Vertreter solcher Quanten-Algorithmen habe ich Ihnen Bereits in meinem Artikel „Anwendungen für Quantencomputer“ vorgestellt: Dem „Quantum Adiabatic Algorithm“ (QAA), dem „Variational Quantum Eigensolver“ (VQE) und dem „Quantum Approximate Optimization Algorithm“ (QAOA). Die aktuelle Forschung für das Machine Learning mit Quantencomputern versucht diese Konzepte für die eigenen Ziele anzuwenden.

Kommen wir aber erst mal zu dem zweiten wichtigen Schwerpunkt der klassischen Künstlichen Intelligenz und des Machine Learnings:

Supervised Machine Learning und Deep Learning

Ein Herzstück aktueller Algorithmen für künstliche Intelligenz und Machine Learning sind „tiefe“ neuronale Netzwerke (Deep Learning – Netzwerke). Historisch gesehen war das Ziel hier, die Neuronen und Synapsen im Gehirn irgendwie programmatisch nachzuahmen. Herausgekommen ist ein Netzwerk von Knotenpunkten, die über mehrere Schichten miteinander verbunden werden.

Quelle: https://de.wikipedia.org/wiki/Deep_Learning#/media/Datei:MultiLayerNeuralNetworkBigger_english.png

Anhand von beliebigen Eingabe-Daten (z.B. mit Bildern von der Ziffern „1“, Bildern von der Ziffer „2“, …) wird das Netzwerk so eingestellt bzw. „trainiert“, dass es möglichst das gewünschte Ergebnis erkennt (die Ziffer 1, 2, …) ^xiv. Wie die Rohdaten für die Eingabe aufbereitet werden, habe ich Ihnen weiter oben schon anhand des „Datenraumes“ erklärt.

Das klassische Deep Leaning wurde in den 1970er entwickelt aber erst 1986 durch den „Backpropagation-Algorithmus“ revolutioniert: Ein Algorithmus über den das gesamte Netzwerk mit jeder neuen Trainingsrunde besonders effizient nachjustiert werden kann. In den letzten 10-15 Jahren zog dann die Hardware nach und wurde leistungsstark genug für die komplexen Algorithmen. Das Zeitalter von Google und Social Media fügte dann den letzten fehlenden Baustein hinzu: Eine Informationsflut von beurteilten Rohdaten, mit denen die Neuronalen Netze trainiert werden können.

Wie beeindruckend gut das Deep Learning mittlerweile funktioniert, sehen wir z.B. an den selbstfahrenden Autos und an den Sprachassistenten. Warum das ganze Konzept aber so gut funktioniert ist bis heute tatsächlich noch nicht genau verstanden ^xv.

Quantencomputer: Netzstrukturen auf Stereoide

Aber wie kommen jetzt die Quantencomputer ins Spiel?

Auf der einen Seite haben wir also die Deep Learning – Netzwerke. Diese sind sehr komplexe, programmierte Netzstrukturen. Durch eine Trainingsphase werden sie so filigran eingestellt, dass sie neue unbekannte Eingabedaten erfolgreich beurteilen können.

Quantencomputer auf der anderen Seite, sind so etwas wie Netze „auf Stereoide“. In Quanten-Netzen können andersartige Strukturen wie selbstverständlich verwendet werden, die in „normalen“ Netzen nicht denkbar wären. Die Vermutung liegt nahe, dass Quantencomputer dadurch einen Mehrwert gegenüber herkömmlichen Computer erzielen können.

Wem dieser Ansatz zu vage ist, dem sei gesagt, dass die Geschichte der Computerwissenschaften voll von „Schaun wir mal“-Algorithmen ist, die sich in der Praxis unheimlich bewährt haben. Ein Beispiel sind gerade die Deep Learning – Netze selbst.

Edward Farhi und Hartmut Neven von Googles Quantum AI-Team, haben 2018 gerade solche neuronalen Quanten-Netze genauer untersucht, die auf die NISQ-Quantencomputer optimiert sind ^xvi. Diese Strukturen bauen unter anderem auf Farhis oben erwähnten QAOA-Algorithmus auf.

Dabei wendeten Farhi und Neven ihre Algorithmen auch auf den MNIST-Datensatz an. MNIST ist ein öffentlich zugänglicher Datensatz von 55.000 beurteilten Bildern. Jedes Bild zeigt eine handgeschriebene Ziffer zwischen 0 und 9. Die MNIST-Bilder sind der allgemein gebräuchliche Standarddatensatz für Deep Learning – Netze über den die verschiedenen Algorithmen einigermaßen objektiv miteinander verglichen werden können.

Farhi und Neven konnten ihr neuronales Quanten-Netz erfolgreich mit den MNIST-Bildern trainieren. Auf einem Quantensimulator mit gerade mal 17 Qubits! Das ist ein Achtungserfolg und ein erster vielversprechender Anfang. Quantencomputer verdoppeln im Prinzip mit jedem weiteren Qubit ihr Potential. Deshalb besteht die Erwartung, dass jeder neue Quantencomputer auch bei den neuronalen Quanten-Netze deutlich meßbare Verbesserungen erzielen kann.

Das Beispiel zeigt aber auch, wie weit der Weg noch ist, bis die Forschung konkurrenzfähige neuronale Quanten-Netzwerke, geschweige denn real überlegene neuronale Quanten-Netzen konstruiert hat. Einen möglichen Weg zeigen Farhi und Neven auch auf: Hybride Quanten-klassische neuronale Netze. Eine Kombination von klassischen Deep Learning – Netzwerken mit neuronalen Quanten-Netzen. Erstere bereiten die Eingabedaten in handlichere Formen auf. Letztere sollten in der Lage, diese reduzierten und speziell präparierten Daten auch mit wenigen Qubits weiter zuverarbeiten und das Gesamtnetzwerk mit den gewünschten Quanten-Effekten zu „würzen“.

Fußnoten

Wie muss man sich einen Quantencomputer vorstellen?

Quantencomputer tauchen regelmäßig in den Medien auf. Inzwischen ist allgemein bekannt, dass sie ein sehr spannendes Thema sind aber dass die Entwicklung von Quantencomputern noch am Anfang steht.

Ich stoße immer wieder auf die Frage, ob man Quantencomputer schon kaufen kann. Die Antwort darauf lautet: Kleines „Ja“ und großes „Aber“.

Zunächst einmal muss man sich klar machen: Ein Quantencomputer hat nur wenig bis nichts mit einem herkömmlichen Computer gemein. Was ich damit genau meine, erfahren Sie am besten in meinem Artikel „Quantencomputer einfach erklärt“.

Erste Quantencomputer existieren bereits heute schon. Deren Quanten-Prozessoren müssen bis fast zum absoluten Nullpunkt heruntergekühlt werden (dieser liegt bei -273°C). Erst dann werden dessen LC-Schaltkreise supraleitend und somit zu Quanten-Bits (Qubits): Den elementaren Bausteinen der Quantencomputer. Um diesen Temperaturpunkt zu erreichen sind große Kühlaggregate notwendig. Ein Quantencomputer ist deshalb ein großer Aufbau, der bestenfalls in einen großen Schrank passt.

Also nichts für den Schreibtisch.

Wofür sollte man einen Quantencomputer kaufen?

Als Nächstes sollte man sich darüber im Klaren sein, dass Quantencomputer voraussichtlich nur für ganz bestimmte Anwendungen eingesetzt werden, die sehr wichtig aber besonders rechenintensiv sind. Inbesondere für folgende Aufgabengebiete

• für Simulationen für Physik, Quantenchemie, -biologie und Materialforschung
• für Optimierungsaufgaben
• für Künstliche Intelligenz und Machine Learning
• für Lineare Algebra

Mehr darüber erfahren Sie in meinem Artikel „Anwendungen für Quantencomputer“.

Aktuell befindet sich die ganze Branche in einer „Proof-Of-Concept“-Phase. Aktuell verfügbare Quantencomputer funktionieren und können erfolgreich betrieben werden. Derzeit ist der konkrete Nutzen allerdings noch nicht vorhanden. Auf dem Papier wurden superschnelle und sehr vielversprechende Algorithmen für Quantencomputer konstruiert. Diese sind für die aktuellen Minimal-Quantencomputer allerdings zu umfangreich.

Erst in den letzten Jahren hat die Forschung damit begonnen, an Algorithmen zu arbeiten, die für die aktuelle Hardware optimiert sind. Diese müssen sich aber erst noch bewähren.

Eine Investition in Quantencomputer wird sich also eher erst mittelfristig, vielleicht sogar erst langfristig und ganz vielleicht sogar gar nicht auszahlen.

Welche Quantencomputer-Angebote kann man kaufen?

Falls Sie meinen Artikel „Welche Quantencomputer gibt es jetzt schon?“ gelesen haben, haben Sie bereits einen Eindruck davon bekommen, welche Quantencomputer-Hardware schon heute oder in Kürze angeboten wird. Darunter sind die Hersteller

• D-Wave-Systems
• IBM
• Google
• Rigetti-Computing
• Alibaba

In meinem Artikel erkennen Sie auch einen klaren Trend:

Alle Hersteller setzen auf Cloudangebote: Dabei werden die Quantenprogramme per Internet an die Cloud-Quantencomputer zum Hersteller übermittelt. Dort werden sie quasi per Fernsteuerung ausgeführt und die Ergebnisse wieder zurück übermittelt. Diese Fernsteuerung kann von einem PC oder auch von einem firmeneigenen Server erfolgen. Den Zugang in die Quantencomputer-Cloud erhält man per Abo.

Die kanadische Firma D-Wave-Systems bietet die eigene Hardware auch als dedizierten Quantencomputer zum Kauf an: Also einen Quantenserver, der im eigenen Rechenzentrum betrieben werden kann, zu einem Listenpreis von vielen Millionen Dollar. Bislang haben allerdings nur wenige Kunden davon Gebrauch gemacht, darunter die NASA und Google.

Der Techriese IBM plant ein ähnliches Angebot für seine Quantencomputer.

<<   >>

Die Optimierung ist ein breites Anwendungsfeld für Computer im Allgemeinen. Schon in den 1990er Jahren zeichnete sich ab, dass die Optimierung auch ein vielversprechendes Anwendungsgebiet für Quantencomputer sein könnten.

Optimierungsprobleme zeichnen sich formal so aus, dass eine „Kostenfunktion“ gegeben ist. Eine Lösung des Problems optimiert diese Kostenfunktion. Neben den exakten Lösungen sind auch Lösungsnäherungen von Interesse, die das Problem besser optimieren als eine Reihe anderer Kandidaten aber vielleicht nicht die beste Lösung sind.

Optimierungsprobleme sind für Quantencomputer auch deshalb von Interesse, weil viele Problemfamilien für Optimierung bekannt sind, die erwiesener Maßen nur mit viel Anfwand auf einem herkömmlichen Computer zu lösen sind.

Einstufung der Quanten-Algorithmen für Optimierung

Auch für die Optimierung stufe ich die Algorithmen nach Adam Boulands Beispiel in zwei Kriterien ein, die ich auch in anderen Artikeln auf quantencomputer-info.de verwende:

1. Beschleunigung: Der Grad an Beschleunigung gegenüber herkömmlichen Computern (bzw. die Beschleunigung gegenüber den besten bekannten Algorithmen für herkömmliche Computer für dieselbe Anwendung)
2. Verfügbarkeit: Der Zeitpunkt, wann dieser Algorithmus vermutlich verfügbar sein wird

Optimierung mit dem Grover-Algorithmus

Der Grover-Algorithmus ist ein Urgestein der Quantencomputer-Forschung. Für einen Quanten-Algorithmus ist er „einigermaßen verständlich“. Wegen seiner universellen Anwendungen habe ich ihm einen einen eigenen Beitrag auf quantencomputer-info.de gewidmet, unter anderem auch wegen der so grundlegenden Fragestellungen, ob ein Quantencomputer die schwierigen NP-Probleme effizient lösen kann.

Da auch Optimierungsprobleme dazugehören, können wir den Grover-Algorithmus hier ebenfalls auflisten. Er ist im Prinzip ein Suchalgeorithmus, der alle möglichen Lösungskandidaten durchprobieren kann.

Tatsächlich erzielt der Grover-Algorithmus nur eine moderate, quadratische Beschleunigung gegenüber herkömmlichen Suchalgorithmen. Ich erläutere in meinem Spezial-Artikel, dass vermutlich keine schnelleren Suchalgorithmen mit einem Quantencomputer möglich sind. Aus diesem Grund geht die Quantencomputer-Forschung davon aus, dass die schwierigen NP-Probleme mit einem Quantencomputer nicht generell effizient gelöst werden können.

Auf der anderen Seite können selbst quadratische Beschleunigung einen gewaltigen Vorteil bringen. Für herkömmliche Computer wurde in der Vergangenheit z.B. der Algorithmus „Schnelle Fourier-Transformation“ entwickelt. Er beschleunigt die „Normale Fourier-Transformation“ ebenfalls quadratisch. Was es damit auf sich hat, ist an dieser Stelle unwichtig. Was ich aber bemerkenswert finde, ist der Titel den die Schnelle Fourier-Transformation für diese moderate Beschleunigung bekommen hat: „The most important numerical algorithm of our lifetime“ ⁱ.

Wie fast alle Quanten-Algorithmen mit aktuell erwiesener Beschleunigung gegenüber herkömmlichen Computer, ist der Grover-Algorithmus vermutlich zu umfangreich für die NISQ-Quantencomputer der nächsten Generationen.

QAA: Optimierung und dem Quantum Adiabatic Algorithm

Der Quantum Adiabatic Algorithm basiert auf dem Adiabatischen Theorem der Quantenmechanik, das noch aus den Anfangszeiten der Quantenmechanik stammt ⁱⁱ. Das Theorem sagt Folgendes aus:

Wir präparieren ein Quantensystem derart, dass es die Quantenversion von einem Optimierungsproblem mit einer bekannten Lösung ist. Die Qubits sind so eingestellt, dass sie der bekannten Lösung in Bit-Darstellung entsprechen. Wenn wir das Quantensystem „adiabatisch“ also langsam ändern, entspricht es jetzt einem neuen Optimierungsproblem. Im Weiteren nenne ich diesen Verlauf den „adiabatischen Pfad“. Die Qubits werden sich dadurch ebenfalls ändern. Die Clou des Adiabatischen Theorems ist, dass die geänderten Qubits jetzt die Lösung des geänderten Problems darstellen ⁱⁱⁱ! Sie müssen nur noch ausgemessen werden, um die Lösung in Bit-Darstellung zu erhalten.

Dabei ist es unerheblich, wie stark wir das Problem ändern. Es kommt lediglich darauf an, dass wir das System langsam ändern. Das Theorem sagt auch aus, wie langsam man das System ändern müsste. Und gerade das könnte sich in der Anwendung als Problem erweisen.

Der Quantum Adiabatic Algorithm ist untrennbar mit dem Quanten Annealer von D-Wave verbunden. D-Waves Annealer ist eine Hardware-Version des Quantum Adiabatic Algorithm. Er ist speziell auf diesen einen Algorithmus abgestimmt und funktioniert dort genauso wie ich es oben beschrieben habe. Andere bekannte Quanten-Algorithmen können allerdings nicht auf ihm ausgeführt werden.

Universelle Quantencomputer, wie die Quantencomputer von Google, IBM, Rigetti und Alibaba können andererseits prinzipiell sowohl den Quantum Adiabatic Algorithm als auch andere Algorithmen ausführen. Hier wird der Quantencomputer allerdings nicht wirklich zeitlich verändert. Stattdessen wird ein Quantenschaltkreis konstruiert, der diese zeitliche Veränderung simuliert. Und tatsächlich ist der Quantum Adiabatic Algorithm auf einem universellen Quantecomputer eine Anwendung der dynamischen Quantensimulation, also der Hamiltonischen Simulation (s.o.). Aus diesem Grund kann der Quantum Adiabatic Algorithm in absehbarer Zeit nur in abgewandelter Form auf einem NISQ-Quantencomputer ausgeführt werden. Diese abgewandelte Form ist gerader der QAOA, den ich weiter unten vorstellen werden.

Auf D-Waves Quanten Annealer kann der Quantum Adiabatic Algorithm allerdings schon heute ausgeführt werden. Wie erfolgreich gegenüber herkömmlichen Optimierungsmethoden dies dort möglich ist, muss erst die Anwendung zeigen.

D-Wave sieht die Anwendungen für den eigenen Quanten Annealer übrigens wesentlich vielfältiger. Tatsächlich gibt es diverse D-Wave-Kunden, die den Quantum Adiabatic Algorithm für andere Anwendungsfelder wie der Künstlichen Intelligenz, Simulation von Quantensystemen, … eingesetzt haben ^iv.

QAOA: Optimierung mit dem Quantum Approximate Optimization Algorithm

Im Jahr 2014 stellten Edward Farhi et al vom Massachusetts Institute of Technology / MIT einen neuen Algorithmus für Optimierung vor, der speziell für die Quantencomputer der NISQ-Arä abgestimmt ist ^{v vi} .

Die Funktionsweise des Quantum Approximate Optimization Algorithm / QAOA ist sehr ähnlich wie die des VQE, der zufälligerweise im selben Jahr vorgestellt wurde, und den ich Ihnen oben beschrieben habe. Der QAOA ist ebenfalls ein Quanten-klassischer Hybrid-Algorithmus:

1. Die Qubits werden so eingestellt, dass sie einen Kandidaten für die Lösung des Optimierungsproblems darstellen.
2. Mit diesem Kandidaten ermittelt der Quantencomputer die Kostenfunktion des Problems. Mit einem Quantencomputer sollte dies effizient durchführbar sein. Da diese Messung immer auch eine Sache von Wahrscheinlichkeiten ist, wird sie mehrmals durchgeführt und der beste Wert verwendet.
3. Über einen herkömmlichen Computer wird ein neuer Kandidat für die Lösung des Problems anhand des bisherigen Optimierungsverlaufs berechnet.

Farhi et al geben darüber hinaus genaue Strategien vor, wie die Kandidaten für die Lösung zu finden sind. Und darin ähnelt der Quantum Approximate Optimization Algorithm / QAOA wiederum dem Quantum Adiabatic Algorithm ^vii: Die Kandidaten für die Lösung werden derart mit Quantengattern manipuliert, dass sie am Ende nichts anderes sind als eine Stückelung des adiabatischen Pfades für das Problem mit einem universellen Quantencomputer. Wie wir weiter oben gesehen haben, garantiert der Quantum Adiabatic Algorithm, dass dieses Verfahren immer zu der Lösung des Problems führt, falls wir die Stückelung nur extrem detailliert wählen.

Farhi argumentiert nun wie folgt: Selbst wenn wir die Stückelung nur sehr grob wählen, können wir versuchen sie über klassische Methoden zu optimieren. Dafür müssen wir nur prüfen, ob die optimierte Stückelung bessere Kostenwerte im Quantencomputer liefert als die vorherige. So gelangen wir vielleicht nicht zu der besten Optimierung aber zumindest zu einer besseren Lösung. Deshalb nennt Farhi den Quanten-Algorithmus auch „approximate algorithm“. Ein weiterer Vorteil von Farhis Methode ist, dass diese Lösungskandidaten vermutlich effizient auf einem NISQ-Quantencomputer erzeugt werden können.

Ob der QAOA eine Beschleunigung gegenüber herkömmlichen Computern erzielt, ist derzeit noch nicht erwiesen. Allerdings stellte Edward Farhi direkt mit der ersten Veröffentlichung eine bestimmte Klasse von kombinatorischen Optimierungsproblemen vor, die sich mit seinem Algorithmus effizienter lösen lassen als durch den besten Algorithmus für herkömmliche Computer. Mit diesem Ergebnis erzielte er große Aufmerksamkeit ^viii. Eine Gruppe namhafter Informatiker nahm darauhin Farhis Ideen als Vorlage und entwickelten einen neueren noch schnelleren klassischen Algorithmus für diese Problem-Klasse.

Nichts destotrotz werden große Hoffnungen in den QAOA gesetzt. Die Anwendungen für den QAOA werden weiterhin ausgiebig untersucht ^ix. Auf dem Portal arxiv.org für Vorveröffentlichungen zähle ich zwischen Dezember 2018 und Juli 2019 23 Fachartikel zum Thema QAOA.Tendenz steigend.

Fußnoten

<<

>>

Quantencomputer besitzen das Potential unsere Gesellschaft maßgeblich zu verändern.

Was vor über 30 Jahren als visionäres aber aussichtsloses Vermächtnis eines genialen Physikers begann, beginnt in diesen Tagen Wirklichkeit zu werden.

Ziel meiner Seite „quantencomputer-info“ ist es, umfassend und stets aktuell über die rätselhafte Technologie zu informieren. Alles was Sie dafür mitbringen müssen ist eine ordentliche Portion Neugierde.

Quantencomputer: Ein Informationsvakuum

Der Begriff „Quantencomputer“ taucht regelmäßig in den Technologie-Nachrichten der Mainstream-Medien auf. Die vereinzelten, sehr vagen Meldungen die Sie dort finden, können ein klares Bild allerdings nicht einmal annähernd ausreichend vermitteln. Auf der anderen Seite können Sie eine Vielzahl von komplizierten, sehr mathematischen Lehrmaterial von Hochschulen zu Quantencomputern finden. Aktuelle Entwicklungen zur Quantencomputer-Forschung können Sie hauptsächlich nur in noch viel anspruchsvolleren wissenschaftlichen Fachartikeln verfolgen. Das setzt ein ungeheures Vorwissen in der Quantenmechanik und in Mathematik voraus.

Insbesondere für Entscheider in der Technologiebranche wird allerdings irgendwann in den nächsten Jahren der Zeitpunkt kommen, an denen sie entscheiden müssen, ob ihr Unternehmen in die neue Technologie Quantencomputer investieren sollte. Informatiker und IT-ler müssen für sich persönlich abwägen, ob sie sich auf den beschwerlichen Weg machen sollten, um sich Knowhow in dem neuen Bereich „Quantencomputer“ anzueignen. Ein Bereich, der so komplett anders ist als jeder anderer in der Informatik. Und letztendlich werden technikinteressierte Laien mehr über die Technologie wissen wollen, der man wahre Wunder nachsagt.

quantencomputer-info.de soll dabei helfen dieses Informationsvakuum mit Leben zu füllen. Auf den nächsten Seiten werde ich Ihnen ein relativ genaues Verständnis für Quantencomputer vermitteln. Ich werde die Grundlagen erklären und auch gezielt auf Themen aus der aktuellen Entwicklung und Forschung eingehen. Dabei werde ich fast vollständig auf mathematische Formeln verzichten und das Wesen hinter den Quantencomputern eher bildlich beschreiben. Anstatt auf Exaktheit lege ich den Fokus also auf ein sehr gutes, qualitatives Verständnis. Deshalb soll diese Internetseite auch ein Ausgangspunkt sein, um in die so ungeheuer komplizierte Materie einzusteigen und dabei den Wald vor lauter Bäumen noch zu sehen.Sowohl im deutschen als auch im englischsprachigen Raum werden Sie wohl keine zweite Internetseite finden, die diesen Anspruch auf diese Weise erfüllt … Glaube ich zumindest.

Insbesondere werde ich Ihnen folgende Fragen genauer beantworten:

• • • Was genau ist ein Quantencomputer?
    • Wie funktioniert ein Quantencomputer?
    • Warum dieser Hype um Quantencomputer?
    • Welche Quantencomputer gibt es jetzt schon und welche wird es demnächst geben?
    • Was sind die absehbaren Anwendungsgebiete für Quantencomputer?
    • Was genau ist ein „Qubit“?
    • Wie sehen Quantenprogramme eigentlich aus?
    • Was ist die Quanten-Überlegenheit?

Dabei halte ich die Antworten auf diese Fragen aktuell und gehe regelmäßig auf neue Entwicklungen ein.

quantencomputer-info.de: Ein Online-Buch

Meine Internetseite ist zum Einen als Online-Buch gedacht, dass Sie von vorne bis hinten durchlesen können. Mittlerweile umfasst es immerhin über 80 Din A4-Seiten und weit über 150 Referenzen auf wissenschaftliche Artikel und Vorträge, die ich über Jahre hinweg gesammelt habe (dank arxiv.org, Youtube, Wikipedea und Co sogar online frei zugänglich).

Falls Sie lieber gezielt einzelne Artikel lesen, was natürlich auch gut geht, möchte ich Ihnen trotzdem meine Einführung „Quantencomputer einfach erklärt“ ans Herz legen. Auch wenn Sie bereits einige grundlegende Dinge über die Quantencomputer erfahren haben, haben Sie eventuell noch nie einen Eindruck davon bekommen, wie ein Quantencomputer-Programm wirklich aussieht, geschweige denn, wie Sie eines schnell mal selbst online ausprobieren können. Außerdem erkläre ich Ihnen hier auf einfache Weise, wie ein bekannter Such-Algorithmus für Quantencomputer(der „Grover-Algorithmus“) in etwa funktioniert.

Letzteren führe ich dann nochmal viel genauer in dem Spezial-Artikel „Der Grover-Algorithmus und die Suche nach dem heiligen Gral“ aus. Nach der Lektüre können Sie das Programm tatsächlich verstehen, inklusive der merkwürdigen Quanten-Logik! Dabei erkläre ich Ihnen auch, welche Bedeutung der Algorithmus für das vielleicht größte offene Rätsel der Computer-Wissenschaften hat: Dem „P=NP“-Problem, das eines der Eine-Millionen-Dollar-Probleme ist.

Wenn Sie besonders an aktuellen Entwicklungen interessiert sind, sollten Sie meine Artikel „Welche Quantencomputer gibt es jetzt schon?“ und „Anwendungen für Quantencomputer“ lesen. Diese Artikel ergänze und aktualisiere ich regelmäßig. Hier erfahren Sie viel über den aktuellen Stand der Hardware, über die aktuell vielversprechenden Quanten-Algorithmen und über die diversen Cloud-Angebote der Techriesen und deren Teams dahinter. In meinem Zusatz-Artikel „Künstliche Intelligenz und Machine Learning mit Quantencomputern“ erfahren Sie dann u.a., wie eine brillanteTeenagerin im Sommer 2018 der kompletten Forschergemeinde den Boden unter den Füßen weghaut.

Wenn Sie genug Ausdauer haben und noch mehr über das Wesen der Quantencomputer, der Quanten-Logik und überhaupt über die Quantenmechanik erfahren wollen, empfehle ich Ihnen den Artikel „Das Qubit und ein Magier bei Britain has Got Talent“. Hier bekommen Sie unter anderem einen Eindruck davon, wie sehr das ganze Thema an pure Zauberei erinnert … am Beispiel eines berühmten und ziemlich coolen Zaubertricks in der englischen Talentshow. Außerdem „spule“ ich zurück nach Helgoland ins Jahr 1925, zur Geburtsstunde der Quantenmechanik und zu Werner Heisenbergs „Magischen Aufsatz“, und erkläre Ihnen seine berühmte „Unschärferelation“ am Beispiel eines Qubits. Diese und die anderen Erklärungen in dem Artikel, anhand von einfachen Zeigerdiagrammen, sind übrigens über einen längeren Zeitraum hinweg entstanden. In so einer Form hätte ich sie mir tatsächlich auch für mein Physikstudium gewünscht.

Und was Sie auch lesen sollten …

Ach, vergessen Sie es. Wenn ich es mir recht überlege: Vermutlich sollten Sie doch einfach alles lesen.

Aber ich muss Sie warnen. Die Quantenmechanik und somit die Quantencomputer sind auf faszinierende Art und Weise mit Nichts vergleichbar, mit dem Sie sich bisher beschäftigt haben. Um sie zu erfassen ist ein gewisser Aufwand und viel Neugierde notwendig … aber was ich eigentlich sagen will, drückt Morpheus in dem Science-Fiction-Klassiker „Die Matrix“ noch am Besten aus:

„Das ist deine letzte Chance. Danach gibt es kein zurück. Nimm die blaue Pille — die Geschichte endet… Nimm die rote Pille — du bleibst hier im Wunderland und ich werde dir zeigen wie tief das Kaninchenloch reicht.”

Das „Quantencomputer-Zeitalter“

Quantencomputer werden vermutlich nach und nach das Tor zu einer neuen Welt öffnen. Diese Welt wird so bizarr und anders sein, dass die Forschung erst langsam einen Eindruck davon bekommt, was darin möglich sein wird. Es ist die Welt der Quanten-Berechenbarkeit und der Quanten-Komplexität. Durch die Quantencomputer werden die rätselhaften Quanteneffekte für unsere „Ära der Algorithmen“ erschlossen.

Die Erschließung der Quantenmechanik hat bereits das Industriezeitalter im Laufe der letzten 100 Jahre revolutioniert. Bahnbrechende Entwicklungen wie die Halbleiter, Transistoren, Dioden, Laser und viele weitere bilden das Herzstück unserer modernen, technologischen Gesellschaft. In allen möglichen Geräten unseres täglichen Lebens sind sie zu finden (wie den Computern, dem Internet, Smartphones, Fernsehern, …). Diese bahnbrechenden Technologien sind allerdings das Resultat von Quanteneffekten von riesigen Massen von Atomen und Lichtteilchen.

Quantencomputer sind stattdessen so etwas wie die digitale Version der Quantenmechanik: Sie verzahnen und verändern auf filigranste Weise einzelne, elementare Quantenzustände. Die Andersartigkeit der Quantenwelt besitzt das Potential das Wesen von grundlegenden Algorithmen und selbst das Wesen unserer Logik komplett umzukrempeln. Wir werden völlig neue und extrem abgekürzte Rechenwege entdecken und beschreiten können, die sonst unmöglich wären.

Am Beispiel eines Aufzuges an einem Hochhaus, erkennen Sie was ich mit „völlig neue Wege“ meine

Seit über zwei Jahrzehnten findet intensive Forschung zu dem Thema Quantencomputer statt. Erste experimentelle Quantencomputer wurden im Laufe der letzten 20 Jahre in Forschungseinrichtungen gebaut. Längst haben die Tech-Riesen Google, IBM, Microsoft & Co das bahnbrechende Potential der Technologie erkannt und führende Physiker, Informatiker und Mathematiker angeworben, um die Entwicklung der ersten kommerziellen Quantencomputer zu befeuern. Als Resultat stehen jetzt die ersten Quantencomputer in der Cloud.

Verfügbar für jedermann.

Noch unbemerkt von der breiten Öffentlichkeit liefern sich die Tech-Giganten aktuell ein spannendes Wettrennen, welche Gruppe als erstes den nächsten großen Meilenstein erreicht: Der erste Nachweis der „Quantum Supremacy“ oder auf deutsch der „Quanten-Überlegenheit“. Also der erste Quantencomputer, der jeden herkömmlichen Supercomputer für gewisse Berechnungen überflügelt.

Alle Zeichen deuten darauf hin, dass dieser Schritt kurz bevor steht.

Quantencomputer: Der einfachste Weg, die Quantenmechanik zu verstehen lernen

Einen weiteren Punkt finde ich persönlich noch wichtig: Ein Quantencomputer ist letztendlich das einfachste Mehrteilchen-System in der Quantenmechanik. Wenn Sie die Funktionsweise eines Quantencomputers verstanden haben, haben Sie zwischen den Zeilen auch sehr viel über die Quantenmechanik erfahren. Zu grundlegenden Themen der Quantenmechanik ist es dann manchmal nur ein kleiner Schritt. Deshalb werde ich immer wieder auf einige Themen eingehen: Vielleicht haben Sie von dem „Welle-Teilchen-Dualismus“ gehört oder von „Schrödingers Katze“ oder von „Heisenbergs Unschärferelation“, der Existenz von „Paralleluniversen“. Oder was hat die Quantemechanik mit „Wurmlöchern“ im Weltraumzu tun? Wenn Sie die Ausdauer haben, werden Sie hier einiges darüber erfahren.

Ich selbst habe Physik und Mathematik studiert. Seit fast 20 Jahren bin ich jetzt als IT-Berater für große Unternehmen tätig. Meine Faszination für die Quantenphysik habe ich dabei nie verloren. Nicht nur in meinen Augen ist sie wie Zauberei: Nur in echt. Mit den Quantencomputern bekommen wir jetzt die Zauberkästen dazu. Ich verfolge sehr genau, wie diese Entwicklungen langsam Einzug in die IT erhält, und vor einer Weile habe ich beschlossen diesen Weg für mich und für andere zu dokumentieren.

<<     >>

<<     >>

Richard Feynmans Vision

Der Weg zu den ersten Quantencomputern war sehr, sehr steil und glich eher der Erstbesteigung des Mount Everest oder dem Wettlauf zur ersten Mondlandung.

Die Idee wurde zum ersten Mal in den 1970er Jahren erwähnt. Als Urvater des Quantencomputers wird allerdings meistens der legendäre amerikanische Physiker und Nobelpreisträger Richard Feynman genannt. Feynman war einer der bedeutendsten Physiker des 20. Jahrhunderts und seine Ideen hatten viel Gewicht. Unter anderem gab er mit einem berühmten Vortrag „There’s Plenty of Room at the Bottom“ auch den Startschuss für die Nanotechnologie. Seinen Nobelpreis bekam er allerdings für seine Beiträge zur Theorie der Elementarteilchen.

Er schlug im Jahr 1982 vor, eine neue Art von Computer zu entwickeln, die sich die Besonderheiten der Quantenmechanik zu nutzen macht. Ein Quantencomputer. Erst dann wäre man in der Lage, so Feynman, die atomare Welt und somit letztendlich die Natur, erfolgreich zu simulieren und zu berechnen. Zu dem Zeitpunkt erschien die Idee allerdings so absolut aussichtslos, dass sie nicht wirklich weiterverfolgt wurde. In den vorangegangenen Jahrzehnten hatte die Forschung nämlich sämtliche experimentelle Untersuchungen der Quantenphysik durchgeführt, indem sie riesige Massen von Elektronen oder Lichtteilchen untersucht hatte. Die Vorstellung kontrollierte Systeme aus einer handvoll Quantenbausteinen zu erstellen, die darüber hinaus stabil genug wären, um damit exakte Rechnungen durchzuführen, galt den meisten Forschern noch als absolut abwegig.

Warum ist das so schwer?

Die Dekohärenz, der Schrecken der Quantenwelt

Ein wichtiger Grund ist Folgender: Ein Quantencomputer verhält sich nur dann wie ein Quantensystem, wenn er perfekt von seiner Umgebung isoliert ist. Wenn er das nicht ist, passiert nach und nach genau das, was bei der Messung des Endergebnisses eines Quantenprogramms passiert: Das System verliert seine Quanteneigenschaften. Jede kleine Interaktion mit der Umgebung ist wie eine kleine Messung. Das Phänomen bezeichnet man „Dekohärenz“. Die Tatsache, dass es die Dekohärenz gibt ist eine grundlegende Eigenschaft der Quantenmechanik. Dahinter steckt das große Rätsel: Warum sehen wir in unsere Alltagswelt keine Quanteneffekte? Am Ende besteht doch schließlich alles aus Atomen, also Quanten. Aus der Frage haben sich verschiedene Interpretationen der Quantenmechanik entwickelt, und sie ist auch noch fast 100 Jahren später immer noch Gegenstand der aktuellen Forschung ^{i ii}. Die bekanntesten Interpretationen heißen „Kopenhagener Deutung“, die um die Gruppe des dänischen Physikers Niels Bohr sehr nachhaltig vertreten wurde und lange Zeit die führende Interpretation in der Physik war. Die zweite oft vertretene Interpretation heißt die „Viele-Welten-Hypothese“ die von der Existenz von Paralleluniversen handelt.

Für die Entwicklung eines Quantencomputers ist es natürlich sehr schade, dass es die Dekohärenz gibt. Auf der anderen Seite können wir froh sein, dass es sie gibt. Denn ansonsten wäre unsere Welt, also die makroskopische Welt, auch eine Quantenwelt und somit ein sehr sehr schräger Platz zum leben.

Quanten-Fehlerkorrektur

Um die letztendlich unvermeidbare Dekohärenz nachhaltig gering zu halten und lange Quantenprogramme überhaupt erst zu ermöglichen, hat sich in den letzten 20 Jahren ein weiterer Forschungszweig in der Quanteninformation herauskristallisiert: Die Quanten-Fehlerkorrektur. Sie wird aus praktischen Gründen noch auf viele Jahre nicht für aktuelle Quantencomputer verfügbar sein. Dennoch wird die Quanten-Fehlerkorrektur ein Herzstück für zukünftige Quantencomputer sein, sobald sie leistungsstark genug dafür sind.

Ziel der Quanten-Fehlerkorrektur ist es Qubits so geschickt anzuordnen, dass Fehler automatisch bereinigt werden können. Bei herkömmlichen Computern ist diese Aufgabe relativ einfach. Dazu müssen Bits lediglich kopiert werden. Dieser Kopiervorgang ist in der Quantenmechanik schlicht und einfach unmöglich. Dies wurde 1982 durch das „No Cloning Theorem“ ausgeschlossen. Ziel der Quantenfehlerkorrektur ist es deshalb aus mehreren echten Qubits ein einzelnes logisches Qubit zu bilden. Im Verbund verhalten sich diese echten Qubits dann wie ein einzelnes Qubit. Ein Fehler in einem physischen Qubit, das zu diesem Verbund gehört, kann dann durch die anderen Qubits des Verbundes korrigiert werden. Das Interessante dabei ist, dass der gesamte Vorgang der Fehlererkennung und Fehlerkorrektur durchgeführt wird, ohne dass ein Qubit tatsächlich gemessen werden muss.

Das bekannteste Quantenprogramm zur Fehlerkorrektur ist der sogenannte topologische Surface-Code von Alexei Kitaev und verbindet in überraschenderweise ein äußerst abstraktes Teilgebiet der Mathematik mit der Quantenmechanik: Die algebraische Topologie ⁱⁱⁱ.

John Preskill vom California Institute of Technology (Caltech), verriet einmal in einem Vortrag: „Der Tag an dem ich Kitaevs Vortrag hörte, war einer der aufregendsten Tage meiner Karriere“ ^iv. Und das muss schon was heißen: Sie erinnern sich vielleicht an meinen Beitrag über die Quanten-Überlegenheit, wie Preskill die Wette gegen Stephen Hawking gewonnen hatte. Mittlerweile arbeitet Kitaev selbst am Caltech …

Die Quantenfehlerkorrektur sieht auf den ersten Blick vielleicht wie eine besonders knifflige technische Fleißarbeit aus. Auf der einen Seite ist sie das auch. Auf der anderen Seite führt sie uns auf eine Frage die grundlegender nicht sein könnte: Was sind eigentlich Raum und Zeit?

Quantengravitation: Was sind eigentlich Raum und Zeit?

Hinter dem „Klebstoff“ der einen Verbund von physischen Qubits für die Quantenfehlerkorrektur zusammenhält, verbirgt sich nichts anderes als das vielleicht größte Zauberwort der Quantenmechanik. Dem „Entanglement“ oder auf deutsch „Verschränkung“, wie sie früher von Erwin Schrödinger, einem der Gründerväter der Quantenmechanik, bezeichnet wurde.

Albert Einstein bezeichnete sie als „spukhafte Fernwirkung“.

Vor etwa 10 Jahren erkannten Forscher, dass besonders interessante Programme für die Quantenfehlerkorrektur dieselbe Struktur haben, wie eine junge, sehr berühmte Theorie, die aus der Superstring-Theorie hervorgegangen ist, und die die Physiker aktuell so enthusiastisch erforschen wie kaum eine andere: Die „Holographische Dualität“, die möglicherweise erste Quantentheorie für die Gravitation- bzw. die Schwerkraft. Demnach ist die Beziehung von physischen Qubits zu logischen Qubits in einem Quantencomputer dieselbe die auch für die Quantengravitation entscheidend ist ^{v vi}.

Seit Albert Einsteins Relativitätstheorie wissen wir, dass die Gravitation nichts anderes ist als eine Krümmung der Raumzeit. Das Lieblings-Anschauungsobjekt in der Relativitätstheorie ist zum Beispiel ein „Schwarzes Loch“, dass jede Art von Materie auf Nimmerwiedersehen aufsaugt, selbst das Licht. Die Krümmung ist in einem Schwarzen Loch besonders drastisch: Am Rand eines Schwarzen Loches ist die Raumzeit so gekrümmt, dass ein hineinfallender Beobachter zunächst nichts merkt ^vii. Ein anderer Beobachter, der sich in einer festen Umlaufbahn um das Schwarze Loch befindet und die hineinfallenden Person beobachtet, sieht etwas völlig anderes: Am Rand dehnt die Raumzeitkrümmung die Zeit immer mehr. Die hineinfallende Person erscheint deshalb immer mehr abzustoppen und überquert den Rand des Schwarzen Loches tatsächlich nie. Wie ein Filmprojektor, der sich immer langsamer dreht und am Ende den Film ganz stoppt ^viii.

In den 1960er Jahren wurde erkannt, dass Einsteins Krümmungsgleichungen Ähnlichkeiten mit der Strömungslehre von Flüssigkeiten haben. Seitdem wird vermutet, dass die Raumzeitkrümmung, genauso wie die Strömungslehre, nur eine Vogelperspektive von etwas noch viel Grundlegenderem ist. In der Quantengravitation versuchen die Theoretiker deshalb in die Raumzeitkrümmung „hineinzuzoomen“ und die Quantentheorie dahinter zu entdecken. Lange Zeit ohne Erfolg, bis vor zwanzig Jahren dann die so faszinierende Holographische Dualität entdeckt wurde ^ix.

Hinter der Quantengravitation steckt also nichts Geringeres als die Frage:

Was sind eigentlich Raum und Zeit?

Es wird vermutet das dieselben netzartigen Quanten-Verschränkungen dabei eine zentrale Rolle spielen, die auch die Quantenfehlerkorrektur möglich machen ^x.

Erinnern Sie sich an meine Anspielung auf den Film „Die Matrix“ am Ende meiner Einleitung? Ich finde, die Quantengravitation ist so „Matix-mäßig“ wie nur etwas. Ich frage mich dann: Kann es sein, dass unser Eindruck von den vielleicht selbstverständlichsten Größen Raum und Zeit nur ein Resultat der Quantenkomplexität ist? So in etwa wie die thermischen Teilchenbewegungen für uns einen Eindruck von Temperatur entstehen lassen?

Die Quantenfehlerkorrektur ist das endgültige Heilmittel gegen die Dekohärenz in den Quantencomputern. Sie hat allerdings einen großen Haken: Die Fehlerkorrektur erfordert so viele zusätzliche physische Qubits, dass die Quantencomputer der nächsten Jahre ohne sie auskommen werden müssen. Entsprechend kurz müssen die Quantenprogramme sein, die auf ihnen ausgeführt werden.

Die ersten Quantencomputer

Der Shor-Algorithmus schlug also ein wie eine Bombe und löste einen regelrechten Boom in der Quantencomputer-Szene aus. Bis ins Jahr 2010 gelang es der Forschung kleine Quantensysteme immer besser und immer genauer zu isolieren und damit erste experimentelle Quantencomputer zu konstruieren.

2001 erstellte IBM zum ersten Mal ein Quantensystem mithilfe des Effekts der Kernspinresonanz, den Sie übrigens auch als „Kernspin-Röhre“ in der Medizin kennen.

Der Quantencomputer von IBM war in der Lage gezielt den Shor-Algorithmus auszuführen, in dem er die Zahl „15“ in die Primfaktoren „3*5“ zerlegte …

Nein, das soll kein Witz sein.

Was sich zunächst lächerlich anhört, war tatsächlich ein Meilenstein in der Forschung. Er bewies, dass ein Quantencomputer prinzipiell gebaut werden kann und zudem in der Lage ist, das zu jener Zeit vielversprechendste Quantenprogramm auszuführen ^xi.

Die Kernspinresonanz erwies sich jedoch als Sackgasse für die Entwicklung des ersten Quantencomputers und es wurde später sogar in Frage gestellt, ob die Kernspin-Quantencomputer echte Quantencomputer wären.

Im Jahr 2008 gelang es Innsbrucker Forschern einen Verbund von 8 kontrollierten Qubits über eine sogenannte „Ionenfalle“ zu erzeugen. Dieselbe Forschungsgruppe ist übrigens auch im Bereich der Quantenteleportation aktiv, einem weiteren Gebiet der Quanteninformationstheorie ^xii.

2011 kam dann die große Nachricht: Die bis dahin eher unbekannte kanadische Firma „D-Wave-Systems“ bietet den ersten kommerziellen Quantencomputer an.

D-Wave-Systems benannte die Anzahl der Qubits in ihrem Quantencomputer mit sage-und-schreibe 128 Qubits! Wenn Sie sich jetzt nochmal die Liste in meinem vorletzten Beitrag über den Vergleich von Qubits und herkömmlichen Bits anschauen:

• 1 Qubit entspricht 2 herkömmlichen Bits
• 2 Qubits entsprechen 4 herkömmlichen Bits
• 10 Qubits entsprechen 16 herkömmlichen Kilo-Byte
• 20 Qubits entsprechen 16 herkömmlichen Mega-Byte
• 30 Qubits entsprechen 16 herkömmlichen Giga-Byte
• 31 Qubits entsprechen 32 herkömmlichen Giga-Byte (jedes weitere Qubit verdoppelt also die Speichergröße)
• 45 Qubits entsprechen in etwa der Speichergröße des größten aktuellen, herkömmlichen Supercomputers

• 50 Qubits, die „Quanten-Überlegenheit“-Grenze

Die Nachricht über D-Waves Quantencomputer sah also auf den ersten Blick so aus, als wäre damit der Durchbruch erzielt worden. Es kam noch besser: Im Jahr 2013 kauften Google und die NASA für mehrere Millionen Dollar ein Nachfolgemodell von D-Wave mit sagenhaften 512 Qubits!

Die Ära der Quantencomputer hatte also mit Pauken und Trompeten begonnen.

Oder nicht?

Referenzen